【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3).

(1)画出△ABC,并求△ABC的面积.
(2)在平面直角坐标系中平移△ABC,使点C经过平移后的对应点为C'(5,4),平移后△ABC得到△A'B'C',画出平移后的△A'B'C',并写出点A',B'的坐标
(3)P(-3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,-3),则m= n=
参考答案:
【答案】(1)见解析;(2)见解析,A′(﹣1,8),B′(2,1);(3)﹣9,1.
【解析】
(1)根据各点在坐标系中的位置描出各点,并顺次连接即可,面积利用矩形面积减去三角形面积求解;
(2)根据图形平移的性质画出平移后的△A′B′C′,并写出点A′,B′的坐标即可;
(3)根据点平移的性质即可得出m、n的值.
解:
(1)如图,△ABC即为所求
 ;
;
作辅助线,过AF⊥x轴,垂足是F, AE⊥y轴,垂足是E.
△ABC的面积=S矩形AFOE-S△AFE- S△BCO- S△AEC
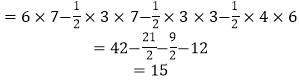
即面积是15.
(2)C(0,3)经过平移后的对应点为C′(5,4),则C点即为,向上平移1个单位,向右平移5个单位,相应的A,B,也一样平移即可得到:如图,△A′B′C′即为所求,A′(﹣1,8),B′(2,1);
(3)∵P(﹣3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,﹣3),
∴n=﹣3+4=1,m+6=﹣3,
∴n=1,m=﹣9.
故答案为:﹣9,1.
-
科目: 来源: 题型:
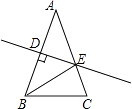
查看答案和解析>>【题目】如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
A.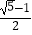
B.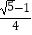
C.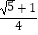
D.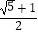
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,tan∠C=
 ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A.18cm2
B.12cm2
C.9cm2
D.3cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下题和解题过程:化简
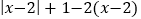 ,使结果不含绝对值.
,使结果不含绝对值.解:当
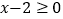 时,即
时,即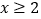 时,
时, 原式

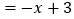 ;
;当
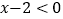 ,即
,即 时,
时,原式
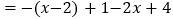
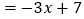
这种解题的方法叫“分类讨论法”.
(1)请你用“分类讨论法”解一元一次方程:
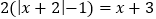 ;
;(2)试探究:当
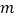 分别为何值时,方程
分别为何值时,方程
①无解,②只有一个解,③有两个解
-
科目: 来源: 题型:
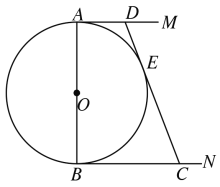
查看答案和解析>>【题目】如图,
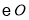 的直径
的直径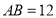 ,
,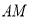 ,
,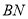 是
是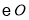 的两条切线,
的两条切线,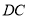 切
切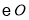 于
于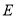 ,交
,交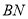 于
于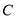 ,设
,设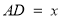 ,
,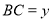 ,
, .
.
(1)求
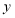 与
与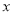 的函数关系式;
的函数关系式;(2)若
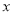 ,
,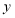 是
是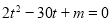 的两实根,求
的两实根,求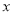 ,
,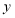 的值;
的值;(3)在(2)的前提下,求
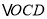 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A(2,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=
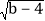 +
+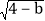 -6
-6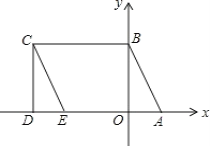
(1)求点C的坐标;
(2)求点E的坐标;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量c关系,并证明你的结论
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=12,AC=
 ,∠B=30°,则△ABC的面积是 .
,∠B=30°,则△ABC的面积是 .
相关试题

