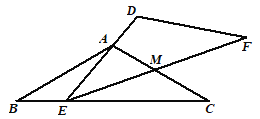
【题目】如图,![]() 和
和![]() 是两个全等的三角形,
是两个全等的三角形,![]() ,
,![]() .现将
.现将![]() 和
和![]() 按如图所示的方式叠放在一起,
按如图所示的方式叠放在一起,![]() 保持不动,
保持不动,![]() 运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
(1)求证:∠BAE=∠MEC;
(2)当E在BC中点时,请求出ME:MF的值;
(3)在![]() 的运动过程中,
的运动过程中,![]() 能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
参考答案:
【答案】(1)证明见解析;(2)见解析;(3)见解析.
【解析】
(1)已知△ABC≌△DEF,根据全等三角形的性质可得∠ABC=∠DEF,又因∠AEC=∠B+∠BAE,∠AEC=∠AEM+∠MEC,即可得∠B+∠BAE=∠AEM+∠MEC,所以∠BAE=∠MEC;(2)当E为BC中点时, AB=AC,根据等腰三角形三线合一的性质可得AE⊥BC,∠EAM=60°,再由∠DEM=30°即可证得AC⊥EF; 在Rt△ABE中,∠B=30°,![]() ,求得BE=
,求得BE=![]() ,即可求得BC=3;在Rt△CEM中,∠C=30°,EC=
,即可求得BC=3;在Rt△CEM中,∠C=30°,EC=![]() E,求得EM=
E,求得EM=![]() ,根据全等三角形的性质可得BC=EF=3,所以FM= EF-EM=
,根据全等三角形的性质可得BC=EF=3,所以FM= EF-EM=![]() ,即可得EM:FM=1:3 ;(3)分AM=AE、EA=EM、
,即可得EM:FM=1:3 ;(3)分AM=AE、EA=EM、![]() 三种情况求解即可.
三种情况求解即可.
(1)证明:∵△ABC≌△DEF
∴∠ABC=∠DEF
∵∠AEC=∠B+∠BAE,∠AEC=∠AEM+∠MEC;
∴∠B+∠BAE=∠AEM+∠MEC,
即∠BAE=∠MEC ;
(2)当E为BC中点时,
∵AB=AC,
∴AE⊥BC,BE=EC=![]() ,∠EAM=60°,
,∠EAM=60°,
又∵∠DEM=30°,
∴AC⊥EF;
∵![]() ,
,![]() ,
,
∴∠B=∠C=30°,
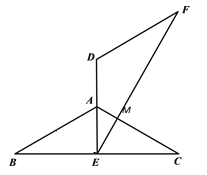
在Rt△ABE中,∠B=30°,![]() ,
,
∴BE=![]() ,
,
∴BC=3;
在Rt△CEM中,∠C=30°,EC=![]() ,
,
∴EM=![]() ,
,
∵△ABC≌△DEF,
∴BC=EF=3,
∴FM= EF-EM=![]() ,
,
∴EM:FM=1:3;
(3)当![]() 或2时,
或2时,![]() 是等腰三角形.
是等腰三角形.
①当![]() 时,如图,
时,如图,

![]()
![]() ,
,
此时点E与点B重合,与题意矛盾(舍去 ) ;
②当![]() 时,如图,
时,如图,

由(1)知,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
③当![]() 时,如图,
时,如图,

则![]() ,
,
![]() ,
,
取BE中点I,连结AI,
则![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
设![]() ,在
,在![]() 中,
中,
由勾股定理,得![]() ,
,
即![]() ,解得
,解得![]()
![]() .
.
综上所述,当![]() 或2时,
或2时,![]() 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
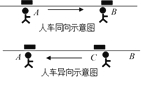
查看答案和解析>>【题目】某人在电车路轨旁与路轨平行的路上骑车行走,他留意到每隔6分钟有一部电车从他后面驶向前面,每隔2分钟有一部电车从对面驶向后面.假设电车和此人行驶的速度都不变(分别为u1, u2表示),请你根据下面的示意图,求电车每隔__________分钟(用t表示)从车站开出一部.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,
 的顶点均在格点上.
的顶点均在格点上.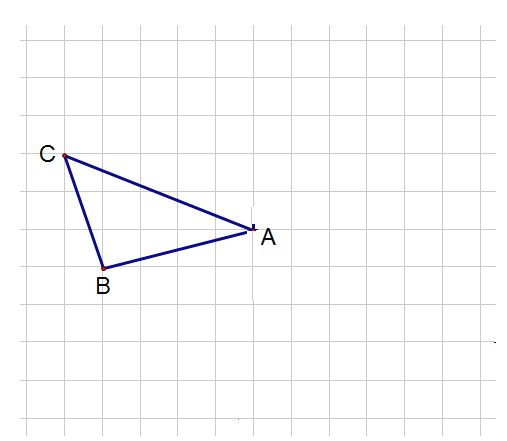
(1)请建立合适的平面直角坐标系,使点
 ,
, 的坐标分别为
的坐标分别为 和
和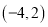 ,并写出点
,并写出点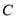 的坐标为___________;
的坐标为___________;(2)在(1)的条件下.①
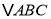 中任意一点
中任意一点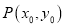 经平移后对应点
经平移后对应点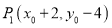 ,将
,将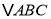 作同样的平移得到
作同样的平移得到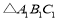 ,请画出
,请画出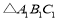 ,并直接写出点
,并直接写出点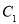 的坐标;
的坐标;②点
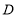 在
在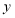 轴上,且
轴上,且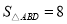 ,则点
,则点 的坐标为__________.
的坐标为__________. -
科目: 来源: 题型:
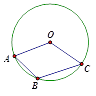
查看答案和解析>>【题目】如图,点A,B,C在⊙O上,已知∠ABC=130°,则∠AOC=( )
A.100°
B.110°
C.120°
D.130° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图8中图①,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向
右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们在学习“实数”时,画了这样一个图,以数轴上的单位长为1的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A,请根据图形回答下列问题:
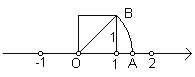
(1)线段OA的长度是___________
(2)这种研究和解决问题的方式,体现了的数学思想方法( ).
A.数形结合B.归纳C.换元D.消元
(3)计算:
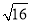 ﹣
﹣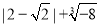 .
.
相关试题

