【题目】观察下列等式,并回答有关问题:![]() ;
;![]() ;
;![]() ;
;
…
(1)若n为正整数,猜想13+23+33+…+n3的值;
(2)利用上题的结论比较13+23+33+…+1003与50002的大小.
参考答案:
【答案】解:(1)根据所给的数据可得:
13+23+33+…+n3=![]() .
.
故答案为:![]() .
.
(2)13+23+33+…+1003=![]()
=![]()
=50502>50002 ,
则13+23+33+…+1003>50002 .
【解析】(1)根据所给的数据,找出变化规律,即是![]() 乘以最后一个数的平方,再乘以最后一个数加1的平方,即可得出答案;
乘以最后一个数的平方,再乘以最后一个数加1的平方,即可得出答案;
(2)根据(1)所得出的规律,算出13+23+33+…+1003的结果,再与50002进行比较,即可得出答案.
【考点精析】认真审题,首先需要了解有理数的乘方(有理数乘方的法则:1、正数的任何次幂都是正数2、负数的奇次幂是负数;负数的偶次幂是正数;注意:当n为正奇数时: (-a)n=-an或(a -b)n=-(b-a)n , 当n为正偶数时: (-a)n =an 或 (a-b)n=(b-a)n).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式6a3﹣54a分解因式的结果为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.在农村电网改造中,四个自然村分别位于如图所示的A,B,C,D处,现计划安装一台变压器,使到四个自然村的输电线路的总长最短,那么这个变压器应安装在AC,BD的交点E处,你知道这是为什么吗?
-
科目: 来源: 题型:
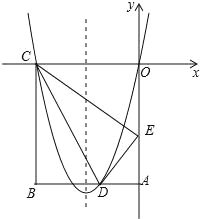
查看答案和解析>>【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=
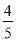 ,反比例函数y=
,反比例函数y=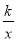 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.(1)求反比例函数解析式;
(2)若函数y=3x与y=
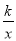 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.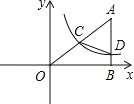
-
科目: 来源: 题型:
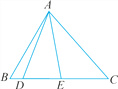
查看答案和解析>>【题目】如图,图中共有_______个三角形,以AD为边的三角形有_________________,以E为顶点的三角形有___________,∠ADB是______的内角,△ADE的三个内角分别是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC≌△DEF,AB=DE,∠A=70°,∠E=30°,则∠F的度数为 ( )
A、 80° B、 70° C、 30 ° D、 100°
相关试题

