【题目】某汽车租赁公司拥有20辆汽车。据统计,当每辆车的日租金为400元时,可全部租出;当辆车的日租金每增加50元时,未租出的车将增加1辆;公司平均每日的各项支出共4800元。设公司每日租出![]() 辆车,日收益为
辆车,日收益为![]() 元,(日收益=日租金收入-平均每日各项支出)。
元,(日收益=日租金收入-平均每日各项支出)。
(1)公司每日租出![]() 辆车时,每辆车的日租金为 元(用含
辆车时,每辆车的日租金为 元(用含![]() 的代数式表示);
的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
参考答案:
【答案】(1)1400-50![]() ;
;
(2)当日租出14辆时,租赁公司收益最大,最大值是5000元
(3)当日租出4辆时,租赁公司日收益不盈也不亏。
【解析】试题分析:(1)根据当全部未租出时,每辆租金为:400+20×50=1400(元),得出公司每日租出x辆车时,每辆车的日租金为:1400-50x;
(2)根据已知得到的二次函数关系求得日收益的最大值即可;
(3)要使租赁公司日收益不盈也不亏,即:y=0.即:-50 (x-14)2+5000=0,求出即可.
试题解析:(1)∵某汽车租赁公司拥有20辆汽车。据统计,当每辆车的日租金为400元时,可全部租出;
当每辆车的日租金每增加50元,未租出的车将增加1辆;
∴当全部未租出时,每辆租金为:400+20×50=1400(元),
∴公司每日租出x辆车时,每辆车的日租金为:(140050x);
故答案为:(140050x);
(2)根据题意得出:
y=x(50x+1400)4800,=50x2+1400x4800,=50(x14)2+5000.
∵50<0,
∴该抛物线的开口方向向下,
∴该函数有最大值。
当x=14时,在范围内,y有最大值5000.
∴当日租出14辆时,租赁公司日收益最大,最大值为5000元。
(3)要使租赁公司日收益不盈也不亏,即:y=0.
即:50(x14)2+5000=0,
解得x1=24,x2=4,
∵x=24不合题意,舍去。
∴当日租出4辆时,租赁公司日收益不盈也不亏。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF ②△ABE∽△ACD,③BE+DC>DE④BE2+DC2=DE2,其中正确的有( )个
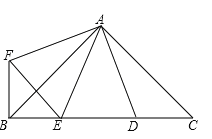
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
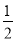 x2+bx+c与y轴交于点C(0,-4),与x轴交于A、B,且点B的坐标为(2,0).
x2+bx+c与y轴交于点C(0,-4),与x轴交于A、B,且点B的坐标为(2,0).(1)求该抛物线的解析式;
(2) 若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值;
(3) 若点D为OA的中点,点M是线段AC上一点,且△OMD是等腰三角形,求M点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C,D,PE是⊙O的切线,E为切点,连接AE,交CD于点F.
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA=
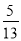 ,求EF的长.
,求EF的长.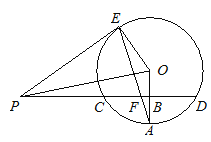
-
科目: 来源: 题型:
查看答案和解析>>【题目】点 A2, 3关于原点的对称点的坐标是( )
A. 2, 3 B. 2, 3 C. 2, 3 D. 3, 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程x2+3=4x配方,得( )
A.(x-2)2=7B.(x+2)2=21C.(x-2)2=1D.(x+2)2=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=
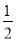 BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④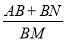 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.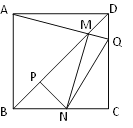
相关试题

