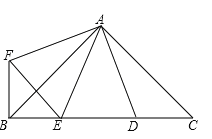
【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF ②△ABE∽△ACD,③BE+DC>DE④BE2+DC2=DE2,其中正确的有( )个
A.1 B.2 C.3 D.4
参考答案:
【答案】C.
【解析】
试题解析:①∵∠DAF=90°,∠DAE=45°,
∴∠FAE=∠DAF-∠DAE=45°.
在△AED与△AEF中,
 ,
,
∴△AED≌△AEF(SAS),①正确;
②∵∠BAC=90°,AB=AC,
∴∠ABE=∠C=45°.
∵点D、E为BC边上的两点,∠DAE=45°,
∴AD与AE不一定相等,∠AED与∠ADE不一定相等,
∵∠AED=45°+∠BAE,∠ADE=45°+∠CAD,
∴∠BAE与∠CAD不一定相等,
∴△ABE与△ACD不一定相似,②错误;
③∵∠BAC=∠DAF=90°,
∴∠BAC-∠BAD=∠DAF-∠BAD,即∠CAD=∠BAF.
在△ACD与△ABF中,
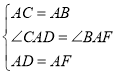 ,
,
∴△ACD≌△ABF(SAS),
∴CD=BF,
由①知△AED≌△AEF,
∴DE=EF.
在△BEF中,∵BE+BF>EF,
∴BE+DC>DE,③正确;
④由③知△ACD≌△ABF,
∴∠C=∠ABF=45°,
∵∠ABE=45°,
∴∠EBF=∠ABE+∠ABF=90°.
在Rt△BEF中,由勾股定理,得BE2+BF2=EF2,
∵BF=DC,EF=DE,
∴BE2+DC2=DE2,④正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值: ①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.
其中会随点P的移动而变化的是( )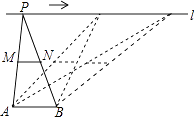
A.②③
B.②⑤
C.①③④
D.④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】-8的立方根是( )
A. -2B. -4C. 2D. ±2
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲班有54人,乙班有48人,要使甲班人数是乙班的2倍,设从乙班调往甲班人数x,可列方程( )
A.54+x=2(48﹣x)
B.48+x=2(54﹣x)
C.54﹣x=2×48
D.48+x=2×54 -
科目: 来源: 题型:
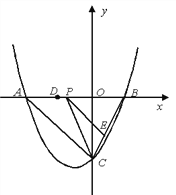
查看答案和解析>>【题目】如图,抛物线y=
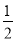 x2+bx+c与y轴交于点C(0,-4),与x轴交于A、B,且点B的坐标为(2,0).
x2+bx+c与y轴交于点C(0,-4),与x轴交于A、B,且点B的坐标为(2,0).(1)求该抛物线的解析式;
(2) 若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值;
(3) 若点D为OA的中点,点M是线段AC上一点,且△OMD是等腰三角形,求M点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C,D,PE是⊙O的切线,E为切点,连接AE,交CD于点F.
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA=
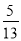 ,求EF的长.
,求EF的长.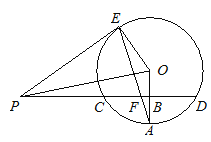
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车租赁公司拥有20辆汽车。据统计,当每辆车的日租金为400元时,可全部租出;当辆车的日租金每增加50元时,未租出的车将增加1辆;公司平均每日的各项支出共4800元。设公司每日租出
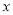 辆车,日收益为
辆车,日收益为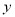 元,(日收益=日租金收入-平均每日各项支出)。
元,(日收益=日租金收入-平均每日各项支出)。(1)公司每日租出
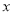 辆车时,每辆车的日租金为 元(用含
辆车时,每辆车的日租金为 元(用含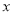 的代数式表示);
的代数式表示);(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
相关试题

