【题目】数学兴趣小组几名同学到商场调查发现,一种纯牛奶进价为每箱40元,厂家要求售价在40~70元之间,若以每箱70元销售平均每天销售30箱,价格每降低1元平均每天可多销售3箱.
(1)现该商场要保证每天盈利900元,同时又要使顾客得到实惠,那么每箱售价为多少元?
(2)若每天盈利为W元,请利用配方法直接写出每箱售价为多少元时,每天盈利最多.
参考答案:
【答案】(1)当每箱牛奶售价为50元时,平均每天的利润为900元.(2)60元.
【解析】
(1)根据平均每天销售这种牛奶的利润=每箱的利润×销售量,设每箱售价为x元,根据“每天盈利900元”列出方程(x-40)[30+3(70-x)]=900 求解即可;
(2)根据平均每天销售这种牛奶的利润等于每箱的利润×销售量得到W=(x-40)[30+3(70-x)],整理后根据二次函数的性质求解.
(1)解:设每箱售价为x元,根据题意得:
(x-40)[30+3(70-x)]=900
化简得:![]() -120x+3500=0
-120x+3500=0
解得:x1=50或x2=70(不合题意,舍去)
∴x=50
答:当每箱牛奶售价为50元时,平均每天的利润为900元.
(2)由题意得W=(x-40)[30+3(70-x)]
=-3![]() +360x-9600
+360x-9600
![]()
∴当售价为每箱牛奶60元时,每天盈利最多.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平直角坐标系xOy中,直线
 与反比例函数
与反比例函数 的图象关于点
的图象关于点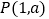

(1)求点P的坐标及反比例函数的解析式;
(2)点
 是x轴上的一个动点,若
是x轴上的一个动点,若 ,直接写出n的取值范围。
,直接写出n的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,数轴上点
 、
、 对应的数分别为
对应的数分别为 、
、 ,且满足
,且满足 ,点
,点 对应点的数为-3.
对应点的数为-3.(1)
 ______,
______, ______;
______;(2)若动点
 、
、 分别从
分别从 、
、 同时出发向右运动,点
同时出发向右运动,点 的速度为3个单位长度/秒;点
的速度为3个单位长度/秒;点 的速度为1个单位长度/秒,求经过多长时间
的速度为1个单位长度/秒,求经过多长时间 、
、 两点的距离为
两点的距离为 ;
;(3)在(2)的条件下,若点
 运动到点
运动到点 立刻原速返回,到达点
立刻原速返回,到达点 后停止运动,点
后停止运动,点 运动至点
运动至点 处又以原速返回,到达点
处又以原速返回,到达点 后又折返向
后又折返向 运动,当点
运动,当点 停止运动点
停止运动点 随之停止运动.求在整个运动过程中,两点
随之停止运动.求在整个运动过程中,两点 ,
, 同时到达的点在数轴上表示的数.
同时到达的点在数轴上表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,对角线AC,BD交于点O,E是AD上任意一点,连接EO并延长,交BC于点F,连接AF,CE.
中,对角线AC,BD交于点O,E是AD上任意一点,连接EO并延长,交BC于点F,连接AF,CE.
(1)求证:四边形AFCE是平行四边形;
(2)若
 ,
, °,
°, .
.①直接写出
 的边BC上的高h的值;
的边BC上的高h的值;②当点E从点D向点A运动的过程中,下面关于四边形AFCE的形状的变化的说法中,正确的是
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形→正方形→平行四边形
C.平行四边形→菱形→平行四边形→菱形→平行四边形
D.平行四边形→菱形→平行四边形→矩形→平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=5cm,BC=10cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以2cm/s的速度运动.点E在线段BC上,且BE=1cm,若M、N两点同时从点D出发,到第一次相遇时停止运动.
(1)求经过几秒钟M、N两点停止运动?
(2)求点A、E、M、N构成平行四边形时,M、N两点运动的时间;
(3)设运动时间为t(s),用含字母t的代数式表示△EMN的面积S(cm2).

-
科目: 来源: 题型:
查看答案和解析>>【题目】当今,人们对健康愈加重视,跑步锻炼成了人们的首要选择,许多与运动有关的手机APP应运而生,聪聪给自己定了目标,每天跑步
 公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:日期
18日
19日
20日
21日
22日
23日
24日
路程(公里)
+1.72
+3.20
—1.91
—0.96
—1.88
+3.30
+0.07
(1)分别用含
 的代数式表示22日及23日的跑步路程;
的代数式表示22日及23日的跑步路程;(2)如图所示是聪聪24日跑步路程是7.07公里,求
 的值;
的值;(3)若跑步一公里消耗的热量为60千卡,请问聪聪跑步七天一共消耗了多少热量?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点P在函数
 的图象上,过P作直线
的图象上,过P作直线 轴于点A,交直线
轴于点A,交直线 于点M,过M作直线
于点M,过M作直线 轴于点B.交函数
轴于点B.交函数 的图象于点Q。
的图象于点Q。(1)若点P的横坐标为1,写出点P的纵坐标,以及点M的坐标;
(2)若点P的横坐标为t,
①求点Q的坐标(用含t的式子表示)
②直接写出线段PQ的长(用含t的式子表示)
相关试题

