Question

【题目】如图，矩形ABCD中，AB=5cm，BC=10cm，动点M从点D出发，按折线DCBAD方向以3cm/s的速度运动，动点N从点D出发，按折线DABCD方向以2cm/s的速度运动．点E在线段BC上，且BE=1cm，若M、N两点同时从点D出发，到第一次相遇时停止运动．

（1）求经过几秒钟M、N两点停止运动？

（2）求点A、E、M、N构成平行四边形时，M、N两点运动的时间；

（3）设运动时间为t（s），用含字母t的代数式表示△EMN的面积S（cm2）．

Answer 1

【答案】（1）经过6 s两点相遇．（2）当点A、E、M、N构成平行四边形时，M、N两点运动的时间为4或4.8s．（3）当0＜t＜时，S =-3t2+t；当≤t＜时，S=S△EMN=EMCD=×（3t-5-1）×5=35-t；当＜t≤5时，S= t-35；当5＜t＜6时，S =15-t．

【解析】

（1）由题意可得：M、N两点同时从点D出发，到第一次相遇时共运动了：2（5+10）=30（cm），则可得t=30÷（2+3）=6；
（2）由题意知，当点N在AD边上运动，点M在BC边上运动时，点A、E、M、N才可能组成平行四边形，然后设经过t秒，四点可组成平行四边形，①当构成AEMN时，10-2t=14-3t，②当构成AMEN时，10-2t=3t-14，继而求得答案；

（3）分别从当 0＜t＜时，当＜时，当t＜5时，当5＜t＜6时，去分析求解即可求得答案．

解：（1）∵矩形ABCD中，AB=5cm，BC=10cm，

∴M、N两点同时从点D出发，到第一次相遇时共运动了：2（5+10）=30（cm），

∴t=30÷（2+3）=6 （s）

答：经过6 s两点相遇．

故答案为：6s.

（2）由题意知，当点N在AD边上运动，点M在BC边上运动时，点A、E、M、N才可能组成平行四边形，

设经过t秒，四点可组成平行四边形，

①当构成AEMN时，10-2t=14-3t，

解得t =4；

②当构成AMEN时，10-2t=3t-14，

解得t=4.8；

答：当点A、E、M、N构成平行四边形时，M、N两点运动的时间为4s或4.8s．

故答案为：4s或4.8s．

（3）如图（1），当0＜t＜时，点M在线段CD上，

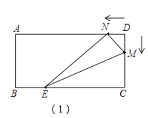
S＝S△EMN =S梯形CDNE-S△DMN-S△CEM=×（2t+9）×5 - ×2t×3t - ×9×（5-3t）=-3t2+t；

如图（2），当≤t＜时，点M在线段CE上，

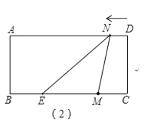
S＝S△EMN=EMCD=×（3t-5-1）×5=35-t；

如图（3），当＜t＜5时，点M在线段BE上，

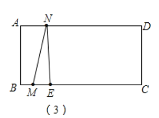
S＝S△EMN=MECD =×（3t-14）×5=t-35；

如图（4），当5＜t＜6时，点M、N都在线段AB上，

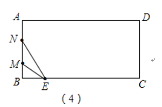
S=S△EMN=MNBE=×（30-2t-3t）×1=15-t．

故答案为：当0＜t＜时，S =-3t2+t；当≤t＜时，S= 35-t；当＜t＜5时，S= t-35；当5＜t＜6时，S =15-t．