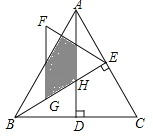
【题目】如图,△ABC是等边三角形,高AD、BE相交于点H,BC=![]() ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
参考答案:
【答案】![]() .
.
【解析】
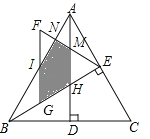
试题分析:如图所示,由△ABC是等边三角形,BC=![]() ,得到AD=BE=
,得到AD=BE=![]() BC=6,∠ABG=∠HBD=30°,由直角三角的性质,得∠BHD=90°﹣∠HBD=60°,由对顶角相等,得∠MHE=∠BHD=60°,由BG=2,得EG=BE﹣BG=6﹣2=4.由GE为边作等边三角形GEF,得FG=EG=4,∠EGF=∠GEF=60°,△MHE是等边三角形;S△ABC=
BC=6,∠ABG=∠HBD=30°,由直角三角的性质,得∠BHD=90°﹣∠HBD=60°,由对顶角相等,得∠MHE=∠BHD=60°,由BG=2,得EG=BE﹣BG=6﹣2=4.由GE为边作等边三角形GEF,得FG=EG=4,∠EGF=∠GEF=60°,△MHE是等边三角形;S△ABC=![]() ACBE=
ACBE=![]() AC×EH×3EH=
AC×EH×3EH=![]() BE=
BE=![]() ×6=2.由三角形外角的性质,得∠BIF=∠FGE﹣∠IBG=60°﹣30°=30°,由∠IBG=∠BIG=30°,得IG=BG=2,由线段的和差,得IF=FG﹣IG=4﹣2=2,由对顶角相等,得∠FIN=∠BIG=30°,由∠FIN+∠F=90°,得∠FNI=90°,由锐角三角函数,得FN=1,IN=
×6=2.由三角形外角的性质,得∠BIF=∠FGE﹣∠IBG=60°﹣30°=30°,由∠IBG=∠BIG=30°,得IG=BG=2,由线段的和差,得IF=FG﹣IG=4﹣2=2,由对顶角相等,得∠FIN=∠BIG=30°,由∠FIN+∠F=90°,得∠FNI=90°,由锐角三角函数,得FN=1,IN=![]() .S五边形NIGHM=S△EFG﹣S△EMH﹣S△FIN=
.S五边形NIGHM=S△EFG﹣S△EMH﹣S△FIN=![]() =
=![]() ,故答案为:
,故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F在OD上一点,且∠1=∠A.
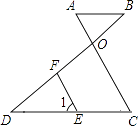
(1)求证:FE∥OC;
(2)若∠DFE=70°,求∠BOC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每个外角都等于60°,则这个多边形的边数为( )
A.8
B.7
C.6
D.5 -
科目: 来源: 题型:
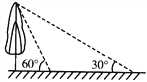
查看答案和解析>>【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法将二次三项式a2+4a﹣5变形,结果是( )
A.(a﹣2)2+9B.(a+2)2+9C.(a﹣2)2﹣9D.(a+2)2﹣9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=﹣2x﹣2.
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知同一平面内,∠AOB=90゜,∠AOC=60゜.

(1)填空:∠COB=;
(2)如OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为;
(3)试问在(2)的条件下,如果将题目中∠AOC=60゜改成∠AOC=2α(α<45゜),其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
相关试题

