【题目】如图,已知同一平面内,∠AOB=90゜,∠AOC=60゜.
(1)填空:∠COB=;
(2)如OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为;
(3)试问在(2)的条件下,如果将题目中∠AOC=60゜改成∠AOC=2α(α<45゜),其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
参考答案:
【答案】
(1)解:分为两种情况::①如图1,当射线OC在∠AOB内部时,∠COB=∠AOB﹣∠AOC=90°﹣60°=30°;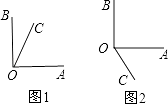 ②如图2,当射线OC在∠AOB外部时,∠COB=∠AOB+∠AOC=90°+60°=150°;故答案为:150°或30°
②如图2,当射线OC在∠AOB外部时,∠COB=∠AOB+∠AOC=90°+60°=150°;故答案为:150°或30°
(2)解:( 2 )在图3中,∵∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC,∴∠DOC= ![]() ∠BOC=
∠BOC= ![]() ×30°=15°,∠COE=
×30°=15°,∠COE= ![]() ∠AOC=
∠AOC= ![]() ×60°=30°,
×60°=30°,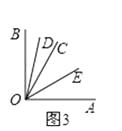
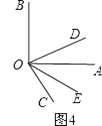 ∴∠DOE=∠COD+∠COE=15°+30°=45°;在图4中,∵∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC,∴∠DOC=
∴∠DOE=∠COD+∠COE=15°+30°=45°;在图4中,∵∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC,∴∠DOC= ![]() ∠BOC=
∠BOC= ![]() ×(90°+60°)=75°,∠COE=
×(90°+60°)=75°,∠COE= ![]() ∠AOC=
∠AOC= ![]() ×60°=30°,∴∠DOE=∠COD﹣∠COE=75°﹣30°=45°;故答案为:45°.
×60°=30°,∴∠DOE=∠COD﹣∠COE=75°﹣30°=45°;故答案为:45°.
(3)解:能求出∠DOE的度数.
①当OC在∠AOB内部时,如图3,

∵∠AOB=90°,∠AOC=2α°,
∴∠BOC=∠AOB﹣∠AOC=90°﹣2α°,
∵OD、OE分别平分∠BOC,∠AOC,
∴∠DOC= ![]() ∠BOC=45°﹣α°,∠COE=
∠BOC=45°﹣α°,∠COE= ![]() ∠AOC=α°,
∠AOC=α°,
∴∠DOE=∠DOC+∠COE=(45°﹣α°)+α°=45°;
②当OC在∠AOB外部时,如图4,

∵∠AOB=90,∠AOC=2α°,
∴∠BOC=∠AOB+∠AOC=90°+2α°,
∵OD、OE分别平分∠BOC,∠AOC,
∴∠DOC= ![]() ∠BOC=45°+α°,∠COE=
∠BOC=45°+α°,∠COE= ![]() ∠AOC=α°,
∠AOC=α°,
∴∠DOE=∠DOC﹣∠COE=(45°+α°)﹣α°=45°;
综合上述,∠DOE=45°
【解析】(1)根据题意分两种情况画出图形:当①如图1,当射线OC在∠AOB内部时,②如图2,当射线OC在∠AOB外部时,分别求出∠BOC的度数。
(2)根据题意分两种情况画出图形:根据已知条件OD平分∠BOC,OE平分∠AOC,分别求出∠DOC,∠COE的度数,然后根据∠DOE=∠COD+∠COE或∠DOE=∠COD﹣∠COE,即可求解。
(3)根据题意分两种情况画出图形:①当OC在∠AOB内部时,如图3,②当OC在∠AOB外部时,如图4,先根据角平分线的定义用含α°的代数式分别表示出∠DOC,∠COE的度数,再根据∠DOE=∠DOC+∠COE和∠DOE=∠DOC﹣∠COE,即可求出结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,高AD、BE相交于点H,BC=
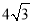 ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .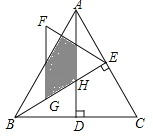
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法将二次三项式a2+4a﹣5变形,结果是( )
A.(a﹣2)2+9B.(a+2)2+9C.(a﹣2)2﹣9D.(a+2)2﹣9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=﹣2x﹣2.
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化? -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程或方程组:
(1)5x+5=9﹣3x;
(2)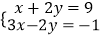 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生利用双休时间去距学校20km的白水寺参观,一部分学生骑自行车先走,过了40min后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,骑车学生的速度是_____________Km/h.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1 , l2 , l3上,且l1 , l2之间的距离为2,l2 , l3之间的距离为3,则AC的长是( )
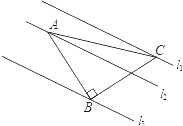
A.
B.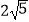
C.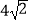
D.7
相关试题

