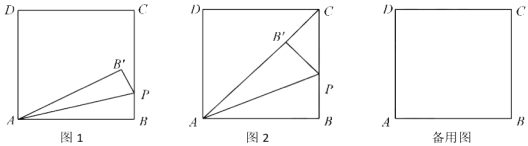
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
参考答案:
【答案】(1)①![]() ;②t=2或t=6或t=2
;②t=2或t=6或t=2![]() (2)见解析.
(2)见解析.
【解析】
(1)①先利用勾股定理求出AC长,再根据△APB≌△APB′,继而根据全等三角形的性质推导得出∠B=∠PB′C=90°,B′C= ![]() ,再证明
,再证明![]() ,根据相似三角形的性质求出PB′=2
,根据相似三角形的性质求出PB′=2![]() -4,由此即可求得答案;
-4,由此即可求得答案;
②根据题意分三种情况,分别画出图形,结合图形分别讨论求解即可;
(2)如图,根据∠PAM=45°以及翻折的性质可以证明得到△DAM≌△B′AM,从而可得AD=AB′=AB,证得四边形ABCD是正方形,继而根据题意画出图形,根据翻折的性质以及全等三角形的知识进行推导即可求得答案.
(1)①∵四边形ABCD是矩形,
∴∠B=90°,
∴AC=![]() ,
,
∵△APB≌△APB′,
∴∠AB′P=∠B=90°,AB′=AB=2![]() ,BP=B′P,
,BP=B′P,
∴∠B=∠PB′C=90°,B′C=AC-AB′=![]() ,
,
又∵∠PCB′=∠ACB,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴PB′=2![]() -4,
-4,
∴PB=2![]() -4,
-4,
即t=2![]() -4;
-4;
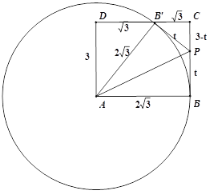
②如图,当∠PCB′=90 °时,此时点B′落在BC上,
在Rt△AB′D中,∠D=90°,∴B′D=![]() ,
,
∴B′C=![]() ,
,
在△PCB′中,由勾股定理得:![]() ,
,
解得t=2;
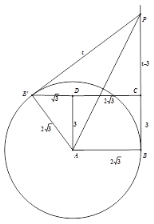
如图,当∠PCB′=90 °时,此时点B′在CD的延长线上,
在Rt△AB′D中,∠ADB′=90°,∴B′D=![]() ,
,
∴B′C=3![]() ,
,
在△PCB′中,由勾股定理得:![]() ,解得t=6;
,解得t=6;
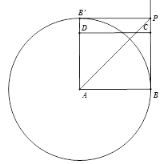
当∠CPB′=90 °时,易得四边形ABPB′为正方形,
∴BP=AB=2![]() ,
,
解得t=2![]() ;
;
综上,t=2或t=6或t=2![]() ;
;
(2)如图
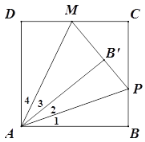
∵∠PAM=45°,
∴∠2+∠3=45°,∠1+∠4=45°,
又∵翻折,
∴∠1=∠2,∠3=∠4,
又∵∠ADM=∠AB′M=90°,AM=AM,
∴△DAM≌△B′AM,
∴AD=AB′=AB,
∴四边形ABCD是正方形,
如图,

设∠APB=x,
∴∠PAB=90°-x,
∴∠DAP=x,
∵AD=AB′,AM=AM,∠ADM=∠AB′M=90°,
∴Rt△MDA≌Rt△B′AM(HL),
∴∠B′AM=∠DAM,
∵翻折,
∴∠PAB=∠PAB′=90°-x,
∴∠DAB′=∠PAB′-∠DAP=90°-2x,
∴∠DAM=![]() ∠DAB′=45°-x,
∠DAB′=45°-x,
∴∠MAP=∠DAM+∠PAD=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△DBC都是边长为2的等边三角形.

(1)以图1中的某个点为旋转中心,旋转△DBC,就能使△DBC与△ABC重合,则满足题意的点为: (写出符合条件的所有点);
(2)将△DBC沿BC方向平移得到△D1B1C1,如图2、图3,则四边形ABD1C1是平行四边形吗?证明你的结论;
(3)在(2)的条件下,当BB1= 时,四边形ABD1C1为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
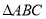 和
和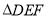 中,
中, ,
,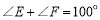 ,将
,将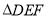 如图放置,使得
如图放置,使得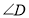 的两条边分别经过点
的两条边分别经过点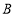 和点
和点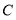 .
.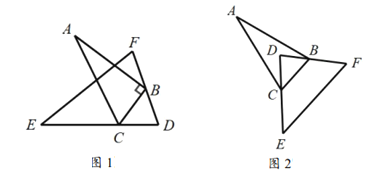
(1)当将
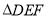 如图1摆放时,
如图1摆放时,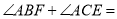 ______
______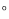 .
.(2)当将
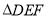 如图2摆放时,试问:
如图2摆放时,试问: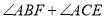 等于多少度?请说明理由.
等于多少度?请说明理由.(3)如图2,是否存在将
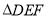 摆放到某个位置时,使得
摆放到某个位置时,使得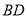 ,
,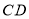 分别平分
分别平分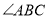 和
和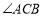 ?如果存在,请画出图形或说明理由.如果不存在,请改变题目中的一个已知条件,使之存在.
?如果存在,请画出图形或说明理由.如果不存在,请改变题目中的一个已知条件,使之存在. -
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为
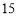 万元/辆,经销一段时间后发现:当该型号汽车售价定为
万元/辆,经销一段时间后发现:当该型号汽车售价定为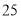 万元/辆时,平均每周售出
万元/辆时,平均每周售出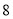 辆;售价每降低
辆;售价每降低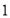 万元,平均每周多售出
万元,平均每周多售出 辆.
辆.(1)当售价为
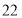 万元/辆时,平均每周的销售利润为___________万元;
万元/辆时,平均每周的销售利润为___________万元;(2)若该店计划平均每周的销售利润是
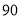 万元,为了尽快减少库存,求每辆汽车的售价.
万元,为了尽快减少库存,求每辆汽车的售价. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂准备用图甲所示的
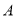 型正方形板材和
型正方形板材和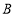 型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.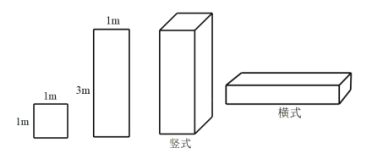
(1)若该工厂准备用不超过2400元的资金去购买
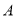 ,
,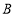 两种型号板材,制作竖式、横式箱子共10个,已知
两种型号板材,制作竖式、横式箱子共10个,已知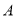 型板材每张20元,
型板材每张20元,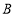 型板材每张60元,问最多可以制作竖式箱子多少只?
型板材每张60元,问最多可以制作竖式箱子多少只?(2)若该工程新购得65张规格为
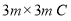 型正方形板材,将其全部切割测好难过
型正方形板材,将其全部切割测好难过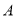 型或
型或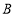 型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,
, 平分
平分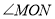 ,点
,点 在射线
在射线 上,
上, 、
、 分别是射线
分别是射线 、
、 上的动点(
上的动点( 、
、 不与点
不与点 重合),连接
重合),连接 交射线
交射线 于点
于点 .设
.设 .
.
(1)如图1,若
 ,则:①
,则:① ______;②当
______;②当 时,
时, ______
______ .
.(2)如图2,若
 ,垂足为
,垂足为 ,则是否存在这样的
,则是否存在这样的 的值,使得
的值,使得 中存在两个相等的角?若存在,求出
中存在两个相等的角?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,△ABC绕点C顺时针旋转得△CEF,当E落在AB边上时,连接BF,取BF的中点D,连接ED,则ED的长是( )
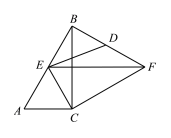
A.2
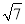 B.4
B.4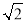 C.6D.4
C.6D.4 
相关试题

