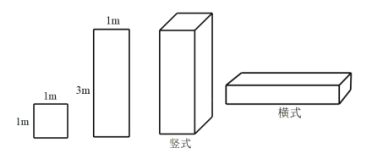
【题目】某工厂准备用图甲所示的![]() 型正方形板材和
型正方形板材和![]() 型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
(1)若该工厂准备用不超过2400元的资金去购买![]() ,
,![]() 两种型号板材,制作竖式、横式箱子共10个,已知
两种型号板材,制作竖式、横式箱子共10个,已知![]() 型板材每张20元,
型板材每张20元,![]() 型板材每张60元,问最多可以制作竖式箱子多少只?
型板材每张60元,问最多可以制作竖式箱子多少只?
(2)若该工程新购得65张规格为![]() 型正方形板材,将其全部切割测好难过
型正方形板材,将其全部切割测好难过![]() 型或
型或![]() 型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
参考答案:
【答案】(1)最多制作竖式箱子5个;(2)45、34、23、12.
【解析】
(1)根据题意可以列出相应的不等式,从而可以求得最多可以制作竖式箱子多少个;
(2)根据题意可以列出相应的二元一次方程,再根据a为整数和a≥10,即可解答本题.
解:(1)由题意可得,
1个竖式箱子需要1个A型和4个B型,1个横式箱子需要2个A型和3个B型,
设竖式箱子x个,则横式箱子(10-x)个,
(20+4×60)x+(2×20+3×60)(10-x)≤2400,
解得,x≤5,
∴x的最大值是5,
答:最多可以制作竖式箱子5个;
(2)如图

C型可以看成三列,每一列可以做成3个A型或1个B型,65个C型就有65×3=195列,
∵材料恰好用完,
∴最后A型的数量一定是3的倍数,
设竖式a个,横式b个,
∵1个竖式箱子需要1个A型和4个B型,1个横式箱子需要2个A型和3个B型,1个B型相当于3个A型,
∴(1+4×3)a+(2+3×3)b=195×3,
∴13a+11b=585,
∵![]() 和
和![]() 都是整数,且
都是整数,且![]() ,
,
解得:![]() 、
、![]() 、
、![]() 、
、![]() ,
,
经验证,四种情况下![]() 型板数量均为3的倍数,
型板数量均为3的倍数,
故答案为:45、34、23、12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
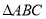 和
和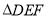 中,
中, ,
,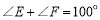 ,将
,将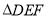 如图放置,使得
如图放置,使得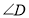 的两条边分别经过点
的两条边分别经过点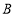 和点
和点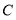 .
.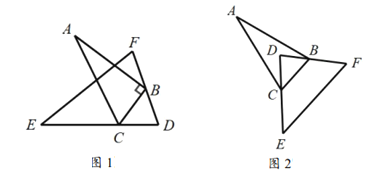
(1)当将
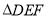 如图1摆放时,
如图1摆放时,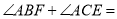 ______
______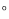 .
.(2)当将
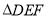 如图2摆放时,试问:
如图2摆放时,试问: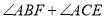 等于多少度?请说明理由.
等于多少度?请说明理由.(3)如图2,是否存在将
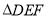 摆放到某个位置时,使得
摆放到某个位置时,使得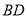 ,
,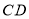 分别平分
分别平分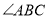 和
和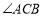 ?如果存在,请画出图形或说明理由.如果不存在,请改变题目中的一个已知条件,使之存在.
?如果存在,请画出图形或说明理由.如果不存在,请改变题目中的一个已知条件,使之存在. -
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为
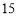 万元/辆,经销一段时间后发现:当该型号汽车售价定为
万元/辆,经销一段时间后发现:当该型号汽车售价定为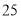 万元/辆时,平均每周售出
万元/辆时,平均每周售出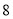 辆;售价每降低
辆;售价每降低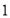 万元,平均每周多售出
万元,平均每周多售出 辆.
辆.(1)当售价为
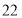 万元/辆时,平均每周的销售利润为___________万元;
万元/辆时,平均每周的销售利润为___________万元;(2)若该店计划平均每周的销售利润是
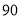 万元,为了尽快减少库存,求每辆汽车的售价.
万元,为了尽快减少库存,求每辆汽车的售价. -
科目: 来源: 题型:
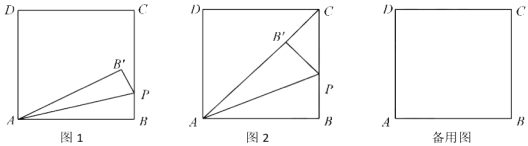
查看答案和解析>>【题目】如图1,在矩形
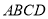 中,BC=3,动点
中,BC=3,动点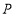 从
从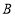 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线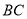 方向移动,作
方向移动,作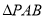 关于直线
关于直线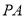 的对称
的对称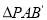 ,设点
,设点 的运动时间为
的运动时间为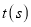
(1)若
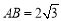
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,
, 平分
平分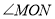 ,点
,点 在射线
在射线 上,
上, 、
、 分别是射线
分别是射线 、
、 上的动点(
上的动点( 、
、 不与点
不与点 重合),连接
重合),连接 交射线
交射线 于点
于点 .设
.设 .
.
(1)如图1,若
 ,则:①
,则:① ______;②当
______;②当 时,
时, ______
______ .
.(2)如图2,若
 ,垂足为
,垂足为 ,则是否存在这样的
,则是否存在这样的 的值,使得
的值,使得 中存在两个相等的角?若存在,求出
中存在两个相等的角?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,△ABC绕点C顺时针旋转得△CEF,当E落在AB边上时,连接BF,取BF的中点D,连接ED,则ED的长是( )
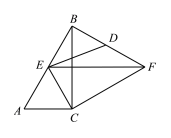
A.2
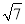 B.4
B.4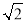 C.6D.4
C.6D.4 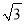
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+2x+3.
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值y为正数时,自变量x的取值范围;
②当﹣2<x<2时,函数值y的取值范围.
相关试题

