【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

参考答案:
【答案】6.
【解析】(1)根据平行四边形的性质得出四边形ABCD是平行四边形,根据垂直推出∠ADC=90°,根据矩形的判定得出即可;
(2)求出DC,根据勾股定理求出AD,根据矩形的面积公式求出即可.
解:(1)证明:∵点O是AC的中点,
∴AO=OC,
∵OE=OD,
∴四边形ADCE是平行四边形,
∵AD是等腰△ABC底边上的高,
∴∠ADC=90°,
∴四边形ADCE是矩形.
(2)∵AD是等腰△ABC底边上的高,BC=16,AB=17,
∴BD=CD=8,AB=AC=17,∠ADC=90°,
由勾股定理得:AD=![]() =
=![]() =15,
=15,
∴四边形ADCE的面积是AD×DC=15×8=120.
“点睛”本题考查了平行四边形的判定,矩形的判定和性质,等腰三角形的性质,勾股定理的应用,能综合运用定理进行推理和计算是解此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠XOY=90°,点A,B分别在射线OX,OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C.试问∠ACB的大小是否变化?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育》的通知,通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A—了解很多”,“B—了解较多”,“C—了解较少”,“D—不了解”),对本市一所中学的学生进行了抽样调查,我们将这次调查的结果绘制成以下两幅统计图.
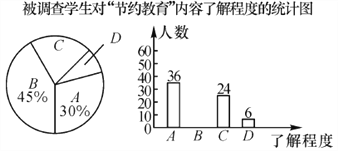
根据以上信息,解答下列问题:
(1)本次抽样调查了多少名学生?
(2)补全两幅统计图;
(3)若该中学共有1 800名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较多”的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F.
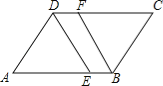
(1)求证:DE=BF;
(2)连接EF,写出图中所有的全等三角形.(不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=(m﹣1)x|m|是正比例函数,则该函数的图象经过第 象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】山东省爱心公益群体为某白血病患者举行了募捐义演晚会,募捐近十万元. 若某中学某班45名学生为该患者捐款315元,且该班同学捐款情况如下表所示,则该班捐款10元的同学有( )
捐款(元)
5
8
10
捐款人数(人)
5
A. 15人 B. 20人 C. 25人 D. 30人
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明某一命题的结论“a<b”时,应假设( )
A.a>b
B.a≥b
C.a=b
D.a≤b
相关试题

