【题目】如图①,在等边![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 边以每秒1个单位的速度向终点
边以每秒1个单位的速度向终点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,以每秒2个单位的速度沿着
出发,以每秒2个单位的速度沿着![]() 方向运动.连结
方向运动.连结![]() ,设点
,设点![]() 运动的时间
运动的时间![]() 秒.
秒.
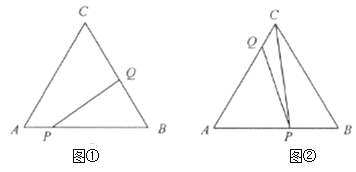
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当![]() 时,求
时,求![]() 的值.
的值.
(3)若![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)如图②,当点![]() 在
在![]() 、
、![]() 之间时,连结
之间时,连结![]() ,
,![]() 被分割成
被分割成![]() 、
、![]() 、
、![]() ,当其中的某两个三角形面积相等时,直接写出
,当其中的某两个三角形面积相等时,直接写出![]() 的值.
的值.
参考答案:
【答案】(1)当0≤![]() ≤3时,
≤3时,![]() ,当3<
,当3<![]() ≤6时,
≤6时,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ;(4)
;(4)![]() 或
或![]()
【解析】
(1)分类讨论:当0≤![]() ≤3时和当3<
≤3时和当3<![]() ≤6时,根据题目意思结合图形解答即可;
≤6时,根据题目意思结合图形解答即可;
(2)根据直角三角形的性质列出方程,解方程得到答案;
(3)作QH⊥AB于H,根据直角三角形的性质用t表示出QH,根据三角形的面积公式解答;
(4)分△APQ的面积=△PCQ的面积、△APQ的面积=△PCB的面积、△CPQ的面积=△PCB的面积三种情况进行讨论.
解:(1)由题意知得:点Q的运动路程为2t,
当0≤![]() ≤3时,
≤3时,![]() ,
,
当3<![]() ≤6时,
≤6时,![]() .
.
(2)∵△ABC为等边三角形,
∴∠A=60°,
当![]() 时,∠QPA=30°,
时,∠QPA=30°,
∴AQ=![]() ,即
,即![]() ,
,
解得![]() .
.
(3)如图①所示,作QH⊥AB于H,

在Rt△QBH中,![]() ,
,
![]() ,
,
如图②所示,作QH⊥AB于H,
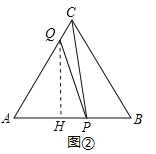
在Rt△QAH中,![]() ,
,
![]() .
.
(4)当点Q为AC的中点时,△APQ的面积=△PCQ的面积,
即12-2t=3,
解得:![]() ,
,
如图①,作CE⊥AB于E,
则![]() ,
,
∴△ABC的面积:![]() ,
,
![]() ,
,
∴△BPC的面积:![]() ,
,
∴△APC的面积:![]() ,
,
![]() ,
,
∴△APQ的面积:![]() ,
,
∴△APC的面积:![]() ,
,
当△APQ的面积=△PCB的面积时,
![]() ,
,
整理得:t2-t+4=0,
△=1-16=-15<0,此方程无解,
当△CPQ的面积=△PCB的面积时,
![]() ,
,
解得:![]() (舍去),
(舍去),
综上所述:在△APQ、△PCQ、△PBC中,其中某两个三角形相等时,![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展“江山如此多娇”为主题的地理知识竞赛活动,要求每班派出一名同学代表本班参赛.九年一班四名同学主动报名,老师为了确定最终参赛人选,对这四名同学的历次地理考试成绩进行了汇总,数据如下:

班级里数学小组的同学对上面的数据进行了进一步的整理:

根据以上的信息,回答下列问题:
(1)写出上表中
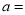 ,
, ,
,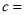 .
.(2)丙同学看到统计表,对老师说:“我的成绩方差最小,说明我的成绩最稳定,应该派我去参赛!”请问你是否同意他的观点?若你是老师,你将派谁参赛?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条河流经过
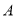 、
、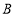 两个港口,水流的速度是4千米/时.甲、乙两船同时出发,由
两个港口,水流的速度是4千米/时.甲、乙两船同时出发,由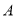 港口顺流驶向
港口顺流驶向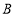 港口,甲船的静水速度快于乙船的静水速度.两船分别到达
港口,甲船的静水速度快于乙船的静水速度.两船分别到达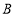 港口后立即返回
港口后立即返回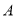 港口.两船与
港口.两船与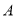 港口的距离
港口的距离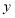 (千米)与出发时间
(千米)与出发时间 (时)之间的函数图像如图所示.
(时)之间的函数图像如图所示.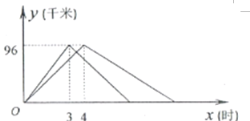
(1)
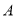 、
、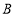 两港口相距 千米.乙船在静水中的速度为 千米/时.
两港口相距 千米.乙船在静水中的速度为 千米/时.(2)求甲船从
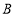 港口返回
港口返回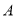 港口时
港口时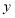 与
与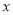 之间的函数关系式.
之间的函数关系式.(3)求两船在途中相遇时,相遇处于
 港口之间的距离.
港口之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】(感知)如图①,正方形
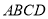 中,点
中,点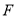 在
在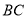 边上,
边上,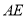 平分
平分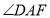 .若我们分别延长
.若我们分别延长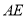 与
与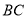 ,交于点
,交于点 ,则易证
,则易证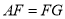 .(不需要证明)
.(不需要证明)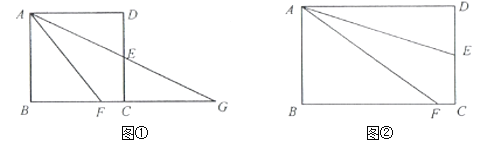
(探究)如图②,在矩形
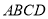 中,点
中,点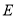 在
在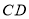 边的中点,点
边的中点,点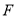 在
在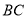 边上,
边上,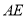 平分
平分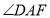 .求证:
.求证: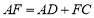 .
.(应用)在(探究)的条件下,若
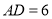 ,
,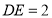 ,直接写出
,直接写出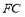 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
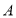 坐标为
坐标为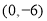 ,点
,点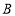 在
在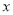 轴的负半轴上,点
轴的负半轴上,点 、
、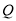 均在线段
均在线段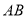 上,且
上,且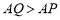 ,点
,点 的横坐标为
的横坐标为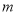 .在
.在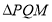 中,若
中,若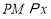 轴,
轴,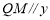 轴,则称
轴,则称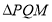 为点
为点 、
、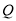 的“榕树三角形”.
的“榕树三角形”.(1)若点
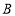 坐标为
坐标为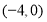 ,且
,且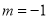 ,则点
,则点 、
、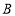 的“榕树三角形”的面积为 .
的“榕树三角形”的面积为 .(2)当点
 、
、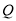 的“榕树三角形”是等腰三角形时,求点
的“榕树三角形”是等腰三角形时,求点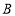 的坐标.
的坐标.(3)在(2)的条件下,作过
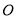 、
、 、
、 三点的抛物线
三点的抛物线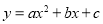 .
.①若
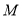 点必为抛物线上一点,求点
点必为抛物线上一点,求点 、
、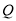 的“榕树三角形”面积
的“榕树三角形”面积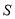 与
与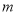 之间的函数关系式.
之间的函数关系式.②当点
 、
、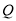 的“榕树三角形”面积2,且抛物线
的“榕树三角形”面积2,且抛物线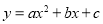 与点
与点 、
、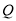 的“榕树三角形”恰有两个交点时,直接写出
的“榕树三角形”恰有两个交点时,直接写出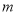 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】容器中有A,B,C 3种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗B粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子.例如,一颗A粒子和一颗B粒子发生碰撞则变成一颗C粒子.现有A粒子10颗,B粒子8颗,C粒子9颗,如果经过各种两两碰撞后,只剩1颗粒子.给出下列结论:
①最后一颗粒子可能是A粒子
②最后一颗粒子一定是C粒子
③最后一颗粒子一定不是B粒子
④以上都不正确
其中正确结论的序号是( ).(写出所有正确结论的序号)
A.①B.②③C.③D.①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
相关试题

