【题目】在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 、
、![]() 均在线段
均在线段![]() 上,且
上,且![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .在
.在![]() 中,若
中,若![]() 轴,
轴,![]() 轴,则称
轴,则称![]() 为点
为点![]() 、
、![]() 的“榕树三角形”.
的“榕树三角形”.
(1)若点![]() 坐标为
坐标为![]() ,且
,且![]() ,则点
,则点![]() 、
、![]() 的“榕树三角形”的面积为 .
的“榕树三角形”的面积为 .
(2)当点![]() 、
、![]() 的“榕树三角形”是等腰三角形时,求点
的“榕树三角形”是等腰三角形时,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,作过![]() 、
、![]() 、
、![]() 三点的抛物线
三点的抛物线![]() .
.
①若![]() 点必为抛物线上一点,求点
点必为抛物线上一点,求点![]() 、
、![]() 的“榕树三角形”面积
的“榕树三角形”面积![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
②当点![]() 、
、![]() 的“榕树三角形”面积2,且抛物线
的“榕树三角形”面积2,且抛物线![]() 与点
与点![]() 、
、![]() 的“榕树三角形”恰有两个交点时,直接写出
的“榕树三角形”恰有两个交点时,直接写出![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)点B的坐标为
;(2)点B的坐标为![]() ;(3)①
;(3)①![]() ;②m=-2或-4≤m≤-3
;②m=-2或-4≤m≤-3
【解析】
(1)待定系数法求直线AB解析式,根据“榕树三角形”新定义和三角形面积即可求出结论;
(2)依据等腰直角三角形性质即可求得点B的坐标;
(3)①先利用待定系数法求得线段AB的表达式,再根据“榕树三角形”新定义求出点M的坐标,再利用三角形面积即可求得S与m之间的函数关系式;
②抛物线![]() 与点
与点![]() 、
、![]() 的“榕树三角形”恰有两个交点时,可分两种情况:点P在对称轴右侧或点P在对称轴左侧(包括对称轴上),分别进行讨论即可.
的“榕树三角形”恰有两个交点时,可分两种情况:点P在对称轴右侧或点P在对称轴左侧(包括对称轴上),分别进行讨论即可.
解:(1)设直线AB解析式为:y=kx+b,则
![]() ,解得
,解得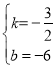
∴直线AB解析式为:![]() ,
,
当x=-1时,![]() ,
,
∴P(-1,![]() ),
),
∵PM∥x轴,BM∥y轴,
∴M(-4, ![]() ),
),
∴PM=3,BM=![]() ,
,
∴![]() .
.
(2)根据题意得,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴点B的坐标为![]() .
.
(3)①首先,确定自变量取值范围为![]() ,
,
由(2)易得,线段![]() 的表达式为
的表达式为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
由于抛物线![]() 经过
经过![]() 、
、![]() 两点,
两点,
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]()
![]() ,
,
![]() ,
,
故![]() ,
,
②∵点P、Q的“榕树三角形”面积为2,
∴![]() ,
,
∴PM=2,
∴M(m-2,-m-6),
∵抛物线![]() 与点
与点![]() 、
、![]() 的“榕树三角形”恰有两个交点,
的“榕树三角形”恰有两个交点,
∴可分两种情况:点P在对称轴右侧或点P在对称轴左侧(包括对称轴上),
若点P在对称轴右侧时,m>-3,此时两个交点关于直线x=-3对称,
∴![]() ,
,
解得:m=-2或m=-4,
∵m>-3,
∴m=-2,
若点P在对称轴左侧(包括对称轴上),即m≤-3,
此时两个交点分别在PM、QM边上,
∴m-2≥-6,即m≥-4,
∴-4≤m≤-3,
综上所述,m的取值范围为m=-2或-4≤m≤-3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条河流经过
 、
、 两个港口,水流的速度是4千米/时.甲、乙两船同时出发,由
两个港口,水流的速度是4千米/时.甲、乙两船同时出发,由 港口顺流驶向
港口顺流驶向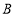 港口,甲船的静水速度快于乙船的静水速度.两船分别到达
港口,甲船的静水速度快于乙船的静水速度.两船分别到达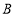 港口后立即返回
港口后立即返回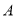 港口.两船与
港口.两船与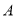 港口的距离
港口的距离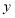 (千米)与出发时间
(千米)与出发时间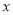 (时)之间的函数图像如图所示.
(时)之间的函数图像如图所示.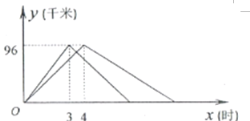
(1)
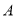 、
、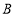 两港口相距 千米.乙船在静水中的速度为 千米/时.
两港口相距 千米.乙船在静水中的速度为 千米/时.(2)求甲船从
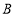 港口返回
港口返回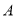 港口时
港口时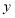 与
与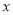 之间的函数关系式.
之间的函数关系式.(3)求两船在途中相遇时,相遇处于
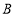 港口之间的距离.
港口之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】(感知)如图①,正方形
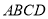 中,点
中,点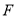 在
在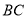 边上,
边上,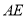 平分
平分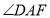 .若我们分别延长
.若我们分别延长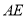 与
与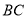 ,交于点
,交于点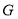 ,则易证
,则易证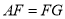 .(不需要证明)
.(不需要证明)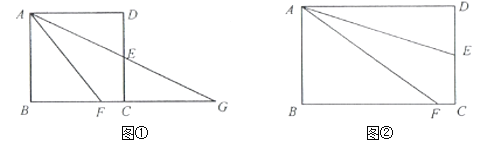
(探究)如图②,在矩形
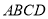 中,点
中,点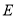 在
在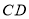 边的中点,点
边的中点,点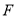 在
在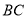 边上,
边上,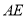 平分
平分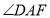 .求证:
.求证: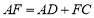 .
.(应用)在(探究)的条件下,若
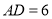 ,
,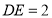 ,直接写出
,直接写出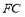 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在等边
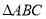 中,
中,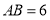 ,动点
,动点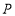 从点
从点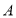 出发,沿
出发,沿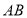 边以每秒1个单位的速度向终点
边以每秒1个单位的速度向终点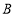 运动,同时动点
运动,同时动点 从点
从点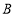 出发,以每秒2个单位的速度沿着
出发,以每秒2个单位的速度沿着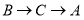 方向运动.连结
方向运动.连结 ,设点
,设点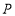 运动的时间
运动的时间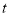 秒.
秒.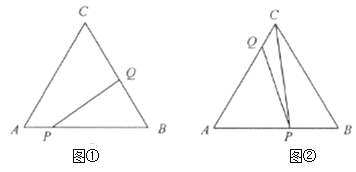
(1)用含
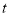 的代数式表示线段
的代数式表示线段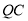 的长.
的长.(2)当
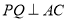 时,求
时,求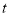 的值.
的值.(3)若
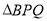 的面积为
的面积为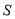 ,求
,求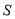 与
与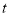 之间的函数关系式.
之间的函数关系式.(4)如图②,当点
 在
在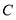 、
、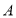 之间时,连结
之间时,连结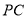 ,
,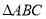 被分割成
被分割成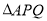 、
、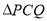 、
、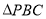 ,当其中的某两个三角形面积相等时,直接写出
,当其中的某两个三角形面积相等时,直接写出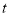 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】容器中有A,B,C 3种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗B粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子.例如,一颗A粒子和一颗B粒子发生碰撞则变成一颗C粒子.现有A粒子10颗,B粒子8颗,C粒子9颗,如果经过各种两两碰撞后,只剩1颗粒子.给出下列结论:
①最后一颗粒子可能是A粒子
②最后一颗粒子一定是C粒子
③最后一颗粒子一定不是B粒子
④以上都不正确
其中正确结论的序号是( ).(写出所有正确结论的序号)
A.①B.②③C.③D.①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接EF并延长,交CB的延长线于点G,连接BD.
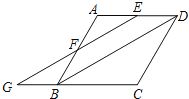
(1) 求证:四边形EGBD是平行四边形;
(2) 连接AG,若∠FGB=
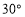 ,GB=AE=3,求AG的长.
,GB=AE=3,求AG的长.
相关试题

