【题目】某校对九年级全体学生进行了一次学业水平测试,成绩评定分为A,B,C,D四个等级(A,B,C,D分别代表优秀、良好、合格、不合格)该校从九年级学生中随机抽取了一部分学生的成绩,绘制成以下不完整的统计图.请你根据统计图提供的信息解答下列问题;
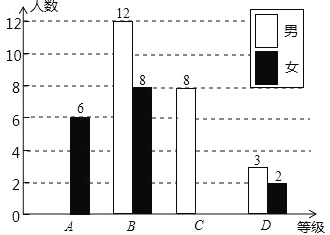
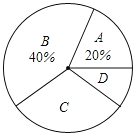
(1)本次调查中,一共抽取了 名学生的成绩;
(2)将上面的条形统计图补充完整,写出扇形统计图中等级C的百分比 .
(3)若等级D的5名学生的成绩(单位:分)分别是55、48、57、51、55.则这5个数据的中位数是 分,众数是 分.
(4)如果该校九年级共有500名学生,试估计在这次测试中成绩达到优秀的人数.
参考答案:
【答案】解:(1)50。
(2)补全条形统计图,如图所示:
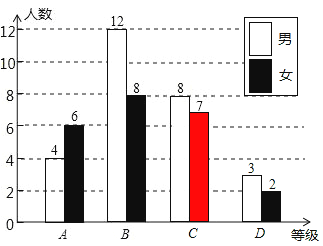
30%。
(3)55;55。
(4)根据题意得:500×20%=100(人),
∴在这次测试中成绩达到优秀的人数有100人。
【解析】
试题分析:(1)根据等级B中男女人数之和除以所占的百分比即可得到调查的总学生数:(12+8)÷40%=50(人)。
(2)根据总学生数乘以A占的百分比求出等级A中男女的学生总数:50×20%=10(人);
进而求出等级A男生的人数:4人;
求出等级D占的百分比:![]() ×100%=10%;
×100%=10%;
确定出等级C占的百分比:1﹣(40%+20%+10%)=30%:
乘以总人数求出等级C的男女之和人数:50×30%=15(人);
进而求出等级C的女生人数:7人。
根据等级C的女生人数7人补全条形统计图即可。
(3)将等级D的五人成绩按照从小到大的顺序排列,48、51、55、55、57,找出最中间的数字55即为中位数,找出出现次数最多的数字55为众数。
(4)用500乘以等级A所占的百分比,即可得到结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且CB=5米.

(1)求钢缆CD的长度;(精确到0.1米)
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
(参考数据:tan400=0.84, sin400=0.64, cos400=
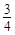 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上有
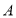 、
、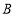 、
、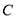 、
、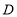 四个点表示的数分别为:-3、-1、2、4,如下图.
四个点表示的数分别为:-3、-1、2、4,如下图.
(1)计算
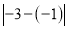 、
、 、
、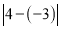 ;再观察数轴,写出
;再观察数轴,写出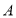 、
、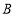 的距离,
的距离,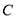 、
、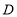 两点的距离,和
两点的距离,和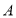 、
、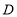 两点的距离.
两点的距离.(2)请用
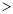 、
、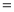 或
或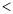 填空:
填空: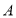 、
、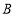 的距离______
的距离______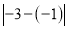 ,
,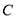 、
、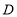 两点的距离______
两点的距离______ ,
,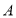 、
、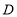 两点的距离______
两点的距离______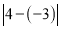 .
.(3)如果点
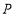 、
、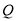 两点表示的数分别为
两点表示的数分别为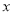 ,
,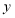 ,那么
,那么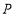 、
、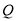 两点的距离=______.
两点的距离=______.(4)若
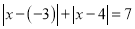 ,数
,数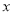 代表的点
代表的点 在数轴上什么位置?
在数轴上什么位置?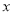 介于哪两个数之间?
介于哪两个数之间? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为18cm2,则S△DGF等于( )
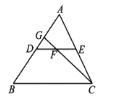
A.4cm2B.5cm2C.6cm2D.7 cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润 2000元。
该加工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨。受人员限制,两种加工方式不可同时进行。受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕。为此,该厂设计了两种可行方案:
方案一:尽可能多地制成奶片,其余直接销售鲜奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成。
你认为哪种方案获利最多?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100
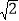 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据: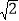 ≈1.41,
≈1.41,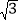 ≈1.73,计算结果保留两位小数)
≈1.73,计算结果保留两位小数)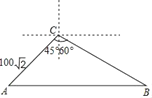
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

相关试题

