【题目】如图,平行四边形ABCD中,E、F分别是边AD,BC的中点.张老师请同学们将纸条的下半部分即平行四边形ABFE沿EF翻折,得到一个V字形图案.
(1)请你在原图中画出翻折后的图形平行四边形A′B′FE(用尺规作图,不写画法,保留作图痕迹)
(2)已知∠A=63°,求∠B′FC的大小.

参考答案:
【答案】(1)图形见解析(2)54°
【解析】试题分析:(1)作∠NFE=∠BFE,∠MEK=∠AEK,然后在EM上截取A′E=AE,在NF上截取B′F=BF,连接A′B′,所得四边形A′B′FE即为所求;
(2)由平行四边形纸条ABCD中,E、F分别为AD、BC的中点,根据平行线分线段成比例定理,可得EF∥AB∥CD,即可求得∠B的度数,又由折叠的性质,即可得∠A=∠B′FE,又由∠B′FC=∠CFE-∠B′FE,即可求得∠B′FC的大小.
试题解析:(1)如图:

(2)∵平行四边形纸条ABCD中,E、F分别为AD、BC的中点,
∴EF∥AB∥CD,
∴∠B=∠CFE=180°﹣∠A=180°﹣63°=117°,
∵平行四边形ABEF沿EF翻折,得到翻折后的平行四边形A′B′FE,
∴∠A=∠B′FE=63°,
∴∠B′FC=∠CFE﹣∠B′FE=117°﹣63°=54°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个函数:
①y=kx(k为常数,k>0)
②y=kx+b(k,b为常数,k>0)
③y=
 (k为常数,k>0,x>0)
(k为常数,k>0,x>0)④y=ax2(a为常数,a>0)
其中,函数y的值随着x值得增大而减少的是( )
A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
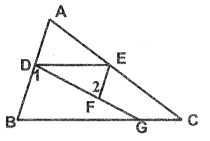
查看答案和解析>>【题目】已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 ∥ ( )
所以∠B+∠BDE=180°( )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180°( )
所以 ∥ ( )
所以∠1=∠2( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
在进行二次根式的化简与运算时,我们有时会碰上如
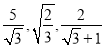 样的式子,其实我们还可以将其进一步化简:
样的式子,其实我们还可以将其进一步化简:(1)
 ···(一)
···(一)(2)
 ···(二)
···(二)(3)
 ···(三)
···(三)以上这种化简的步骤叫做分母有理化.
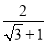 还可以用以下方法化简:
还可以用以下方法化简: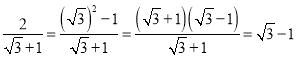 ···(四)
···(四)请完成下列问题:
(1)请计算
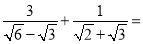 ;
;(2)当
 ,则代数式
,则代数式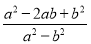 的值为 ;
的值为 ;(3)请参照(三)式和(四)式用两种不同的方法化简
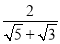
(4)化简:
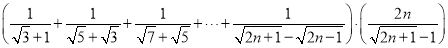
-
科目: 来源: 题型:
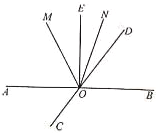
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
(1)若∠MOE=27°,求∠AOC的度数;
(2)当∠BOD=x°(0<x<90)时,求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.

(探究展示)
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
(拓展延伸)
(3)若(2)中矩形ABCD两边AB=6,BC=9,求AM的长.
相关试题

