【题目】为了解中考体育科目训练情况,某区从全区九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格:D级:不及格),并将测试结果绘成了如下两幅不完整的统计图。请根据统计图中的信息解答下列问题:
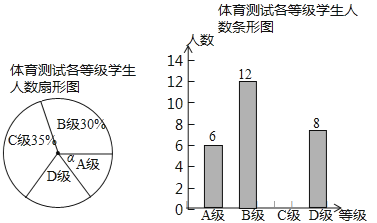
(1)求本次抽样测试的学生人数是多少?
(2)通过计算把图中的条形统计图补充完整
(3)该区九年级有学生7000名,如果全部参加这次中考体育科目测试请估计不及格人数有多少人?
参考答案:
【答案】(1)抽样测试的学生人数是40人;(2)见解析;(3)不及格的人数有1400人.
【解析】
(1)用B级人数12除以B及人数占的百分比即可;
(2)用(1)中求得的数据乘以35%即可求出C级人数,然后补全统计图即可;
(3)用7000乘以D级人数的百分比即可.
解:(1)12÷30%=40(人),
∴本次抽样测试的学生人数是40人;
(2)40×35%=14(人),
∴抽样测试中为C级的人数是14人,
补全条形统计图,如图所示;
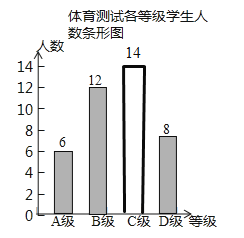
(3)7000×![]() =1400(人),
=1400(人),
∴估计不及格的人数有1400人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数” .将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123) =6.
(1)计算:F(315),F(746);
(2)若s、t都是“相异数”,其中s=100x+42,t=160+y(1≤x≤9,1≤y≤9,x、y都是正整数),当F(s)+F(t)=17时,求x、y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且
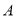 (0,3)、
(0,3)、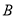 (﹣4,0).
(﹣4,0).(1)求经过点
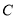 的反比例函数的解析式;
的反比例函数的解析式;(2)设
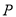 是(1)中所求函数图象上一点,以
是(1)中所求函数图象上一点,以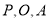 顶点的三角形的面积与△COD的面积相等.求点P的坐标.
顶点的三角形的面积与△COD的面积相等.求点P的坐标.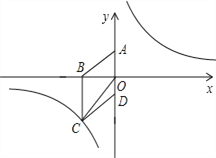
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 分别与直线AB、
分别与直线AB、 相交于点
相交于点 、
、 ,
, 与
与 互补,
互补, 的平分线与
的平分线与 的平分线交于点
的平分线交于点 ,与直线
,与直线 交于点
交于点 ,
, 交
交 于点
于点 ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
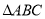 中,
中, 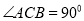 ,点
,点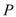 到
到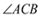 两边的距离相等,且
两边的距离相等,且 .
.(1)先用尺规作出符合要求的点
 (保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;(2)设
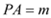 ,
,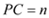 ,试用
,试用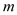 、
、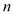 的代数式表示
的代数式表示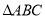 的周长和面积;
的周长和面积;(3)设
 与
与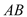 交于点
交于点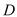 ,试探索当边
,试探索当边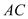 、
、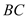 的长度变化时,
的长度变化时,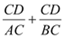 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O是△ABC的外接圆,AB是直径,过
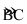 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2
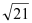 ,求AC的长.
,求AC的长.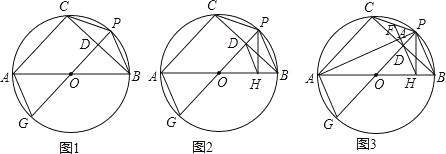
-
科目: 来源: 题型:
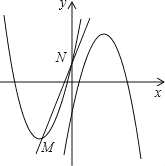
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线C1:y=
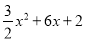 的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.(1)结合图象,直接写出不等式
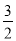 x2+6x+2<kx+b的解集;
x2+6x+2<kx+b的解集;(2)若抛物线C2的顶点与点M关于原点对称,求p的值及抛物线C2的解析式;
(3)若直线l沿y轴向下平移q个单位长度后,与(2)中的抛物线C2存在公共点,
求3﹣4q的最大值.
相关试题

