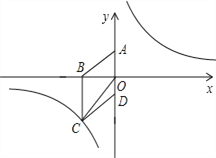
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且![]() (0,3)、
(0,3)、![]() (﹣4,0).
(﹣4,0).
(1)求经过点![]() 的反比例函数的解析式;
的反比例函数的解析式;
(2)设![]() 是(1)中所求函数图象上一点,以
是(1)中所求函数图象上一点,以![]() 顶点的三角形的面积与△COD的面积相等.求点P的坐标.
顶点的三角形的面积与△COD的面积相等.求点P的坐标.
参考答案:
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,
, ![]() )或(-
)或(-![]() ,-
,-![]() ).
).
【解析】试题分析:综合考查反比例函数及菱形的性质,注意:根据菱形的性质得到点C的坐标;点P的横坐标的有两种情况.
(1)根据菱形的性质可得菱形的边长,进而可得点C的坐标,代入反比例函数解析式可得所求的解析式; (2)设出点P的坐标,易得△COD的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,就求得了点P的坐标.
试题解析:(1)由题意知,OA=3,OB=4,
在Rt△AOB中,AB=![]() =5,
=5,
∵四边形ABCD为菱形,
∴AD=BC=AB=5,
∴C(-4,-5).
设经过点C的反比例函数的解析式为y=![]() (k≠0),
(k≠0),
则![]() =-5,解得k=20.
=-5,解得k=20.
故所求的反比例函数的解析式为y=![]() .
.
(2)设P(x,y),
∵AD=AB=5,OA=3,
∴OD=2,S△COD=![]() ×2×4=4,
×2×4=4,
即![]() OA|x|=4,
OA|x|=4,
∴|x|=![]() ,
,
∴x=±![]() ,、
,、
当x=![]() 时,y=
时,y=![]() =
=![]() ,当x=-
,当x=-![]() 时,y=
时,y=![]() =-
=-![]() ,
,
∴P(![]() ,
, ![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数” .将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123) =6.
(1)计算:F(315),F(746);
(2)若s、t都是“相异数”,其中s=100x+42,t=160+y(1≤x≤9,1≤y≤9,x、y都是正整数),当F(s)+F(t)=17时,求x、y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 分别与直线AB、
分别与直线AB、 相交于点
相交于点 、
、 ,
, 与
与 互补,
互补, 的平分线与
的平分线与 的平分线交于点
的平分线交于点 ,与直线
,与直线 交于点
交于点 ,
, 交
交 于点
于点 ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解中考体育科目训练情况,某区从全区九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格:D级:不及格),并将测试结果绘成了如下两幅不完整的统计图。请根据统计图中的信息解答下列问题:
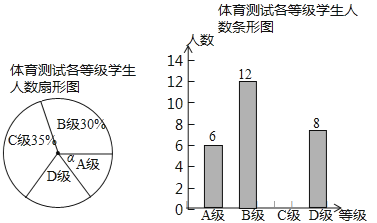
(1)求本次抽样测试的学生人数是多少?
(2)通过计算把图中的条形统计图补充完整
(3)该区九年级有学生7000名,如果全部参加这次中考体育科目测试请估计不及格人数有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
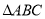 中,
中, 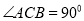 ,点
,点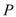 到
到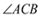 两边的距离相等,且
两边的距离相等,且 .
.(1)先用尺规作出符合要求的点
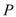 (保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;(2)设
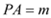 ,
,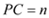 ,试用
,试用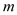 、
、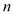 的代数式表示
的代数式表示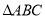 的周长和面积;
的周长和面积;(3)设
 与
与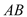 交于点
交于点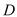 ,试探索当边
,试探索当边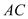 、
、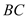 的长度变化时,
的长度变化时,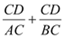 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
相关试题

