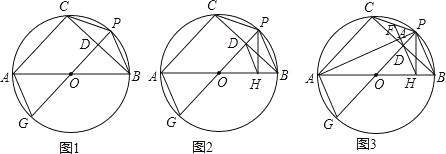
【题目】⊙O是△ABC的外接圆,AB是直径,过![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2![]() ,求AC的长.
,求AC的长.
参考答案:
【答案】(1)证明见解析;
(2)证明见解析;
(3)AC=10
【解析】
试题分析:(1)利用等弧所对的圆周角相等即可求解;
(2)利用等弧所对的圆周角相等,得到角相等∠APG=∠CAP,判断出△BOD≌△POH,再得到角相等,从而判断出线平行;
(3)由三角形相似,得出比例式,△HON∽△CAM,![]() ,再判断出四边形CDHM是平行四边形,最后经过计算即可求解.
,再判断出四边形CDHM是平行四边形,最后经过计算即可求解.
试题解析:(1)∵过![]() 的中点P作⊙O的直径PG,
的中点P作⊙O的直径PG,
∴CP=PB,
∵AB,PG是相交的直径,
∴AG=PB,
∴AG=CP;
(2)证明:如图 2,连接BG
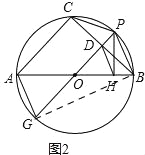
∵AB、PG都是⊙O的直径,
∴四边形AGBP是矩形,
∴AG∥PB,AG=PB,
∵P是弧BC的中点,
∴PC=BC=AG,
∴弧AG=弧CP,
∴∠APG=∠CAP,
∴AC∥PG,
∴PG⊥BC,
∵PH⊥AB,
∴∠BOD=90°=∠POH,
在△BOD和△POH中,
 ,
,
∴△BOD≌△POH,
∴OD=OH,
∴∠ODH=![]() (180°﹣∠BOP)=∠OPB,
(180°﹣∠BOP)=∠OPB,
∴DH∥PB∥AG.
(3)如图3,作CM⊥AP于M,ON⊥DH于N,
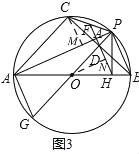
∴∠HON=![]() ∠BOP=
∠BOP=![]() ∠COP=∠CAP,
∠COP=∠CAP,
∴△HON∽△CAM,
∴![]() ,
,
作PQ⊥AC于Q,
∴四边形CDPQ是矩形,
△APH与△APQ关于AP对称,
∴HQ⊥AP,
由(1)有:HK⊥AP,
∴点K在HQ上,
∴CK=PK,
∴PK是△CMP的中位线,
∴CM=2FK=4,MF=PF,
∵CM⊥AP,HK⊥AP,
∴CM∥HK,
∴∠BCM+∠CDH=180°,
∵∠BCM=∠CAP=∠BAP=∠PHK=∠MHK,
∴∠MHK+∠CDH=180°,
∴四边形CDHM是平行四边形,
∴DH=CM=4,DN=HN=2,
∵S△ODH=![]() DH×ON=
DH×ON=![]() ×4×ON=2
×4×ON=2![]() ,
,
∴ON=![]() ,
,
∴OH=![]() =5,
=5,
∴AC=![]() =10.
=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过约38万公里、26天的漫长飞行,2019年1月3日10时26分,“嫦娥四号“探测器自主着陆在月球背面南极一艾特肯盆地内的冯,卡门擅击坑内,实现人类探测器的首次月背软着陆,数据38万用科学记数法可表示为( )
A. 0.38×106B. 3.8×107C. 3,8×108D. 3.8×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知当x=-1时,代数式2mx3-3mx+6的值为7,若关于y的方程2my+n=11-ny-m的解为y=2,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.
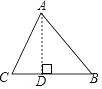
(1)作AD⊥BC于D,设BD=x,用含x的代数式表示CD,则CD=________;
(2)请根据勾股定理,利用AD作为“桥梁”建立方程,并求出x的值;
(3)利用勾股定理求出AD的长,再计算三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把点(2,3)向下平移4个单位长度,得到对应点的坐标是( )
A.(2,7)
B.(6,3)
C.(﹣2,3)
D.(2,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(a-1)-a(a-1); (2)分解因式:xy-4x;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决关于x,y的二元一次方程组
 时,小明由于粗心,把c写错解得
时,小明由于粗心,把c写错解得  ,小红正确地解得
,小红正确地解得  ,求a2b﹣ab2﹣c的值.
,求a2b﹣ab2﹣c的值.
相关试题

