Question

【题目】在△ABC中，AB＝12，AC＝BC＝10，将△ABC绕点A按顺时针方向旋转，得到△ADE，旋转角为α(0°<α<180°)，点B的对应点为D，点C的对应点为E，连接BD，BE．

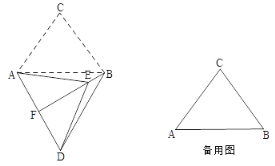
（1）如图，当α＝60°时，延长BE交AD于点F．

①求证：△ABD是等边三角形；

②求证：BF⊥AD，AF＝DF；

③请直接写出BE的长．

（2）在旋转过程中，过点D作DG垂直于直线AB，垂足为G，连接CE，当∠DAG＝∠ACB，且线段DG与线段AE无公共点时，请直接写出BE＋CE的值．

Answer 1

【答案】（1）①证明见解析；②证明见解析；③ BE＝6－8；（2）BE＋CE＝26 ．

【解析】

（1）①由旋转性质知AB=AD，∠BAD=60°即可得证；

②由BA=BD、EA=ED根据线段垂直平分线的性质即可得证；

③分别求出BF、EF的长即可得；

（2）由∠ACB+∠BAC+∠ABC=180°、∠DAG+∠DAE+∠BAE=180°、∠DAG=∠ACB、∠DAE=∠BAC得∠BAE=∠BAC且AE=AC，根据三线合一可得CE⊥AB、AC=10、AH=6，继而知CE=2CH=16、BE=10，即可得答案．

（1）①∵△ABC绕点A顺时针方向旋转60°得到△ADE，

∴AB=AD，∠BAD=60°，

∴△ABD是等边三角形；

②由①得△ABD是等边三角形，

∴AB=BD，

∵△ABC绕点A顺时针方向旋转60°得到△ADE，

∴AC=AE，BC=DE，

又∵AC=BC，

∴EA=ED，

∴点B、E在AD的线段垂直平分线上，

∴BE是AD的线段垂直平分线，

∵点F在BE的延长线上，

∴BF⊥AD，AF=DF；

③由②知BF⊥AD，AF=DF，

∴AF=DF=6，

∵AE=AC=10，

∴EF=8，

∵在等边三角形ABD中，BF=，

∴BE=BF﹣EF=；

（2）如图所示，

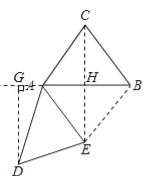
∵∠DAG=∠ACB，∠DAE=∠BAC，

∴∠ACB+∠BAC+∠ABC=∠DAG+∠DAE+∠ABC=180°，

又∵∠DAG+∠DAE+∠BAE=180°，

∴∠BAE=∠ABC，

∵AC=BC=AE，

∴∠BAC=∠ABC，

∴∠BAE=∠BAC，

∴AB⊥CE，且CH=HE=CE，

∵AC=BC，

∴AH=BH=AB=6，

∴CH=

则CE=2CH=16，BE=10，

∴BE+CE=10+16=26．