搜索
【题目】如图1，有一个面积为1的正方形，经过一次“生长”后，在它的左右肩上生出两个小正方形，如图2，其中，三个正方形围成的三角形是直角三角形．再经过一次“生长”后，变成图3；“生长”10次后，如果继续“生长”下去，它将变得更加“枝繁叶茂”．
随着不断地“生长”，形成的图形中所有正方形的面积和也随之变化.若生长n次后，变成的图中所有正方形的面积用Sn表示，求回答：
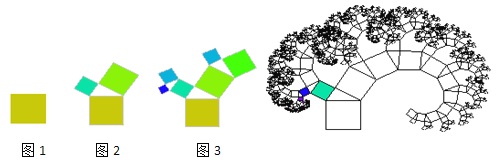
（1）S0＝ ，S1＝ ，S2＝ ，S3＝ ；
（2）S0＋S1＋S2＋…＋S10＝ ．
参考答案：
【答案】（1）1，2，3，4；（2）66.
【解析】试题分析：（1）求出每一次生长后所生长出的四边形面积，找出变化规律即可；
（2）根据（1）中的规律即可得出结论．
解：(1)如图所示，
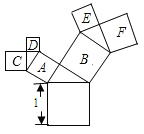
∵正方形的面积为1，
∴第一次生长后长出的三角形面积为SA+SB=1；
第二次生长后长出的三角形面积为SC+SD+SE+SF=1；
第三次生长后长出的三角形面积为：1；
第四次生长后长出的三角形面积为：1；
∴S0=1,S1=2,S2=3,S3=4.
故答案为：1，2，3，4；
(2)根据(1)中的规律可知,S0+S1+S2+…+S10=1+2+3+4+5+6+7+8+9+10+11=66.
故答案为：66.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若三个连续正整数的和小于39，则这样的正整数中，最大的一组数的和是__________
-
科目： 来源： 题型：
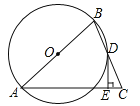
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，点D在BC上，BD=DC，过点D作DE⊥AC，垂足为E，⊙O经过A，B，D三点．
（1）求证：AB是⊙O的直径；
（2）判断DE与⊙O的位置关系，并加以证明；
（3）若⊙O的半径为3，∠BAC=60°，求DE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】第二次全国残疾人抽样调查结果显示，我国0～6岁精神残疾儿童约为11.1万人，11.1万人用科学记数法表示为（ ）
A.1.11×104
B.11.1×104
C.1.11×105
D.1.11×106 -
科目： 来源： 题型：
查看答案和解析>>【题目】课本的作业题中有这样一道题：把一张顶角为36°的等腰三角形纸片剪两刀，分成3张小纸片，使每张小纸片都是等腰三角形，你能办到吗？请画示意图说明剪法．
我们有多少种剪法，图1是其中的一种方法：
定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．
（1）请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）
（2）△ABC中，∠B=30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD=BD，DE=CE，设∠C=x°，试画出示意图，并求出x所有可能的值．
-
科目： 来源： 题型：
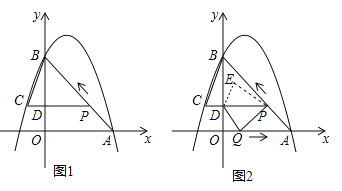
查看答案和解析>>【题目】如图 1，二次函数
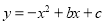的图像过点 A （3，0），B （0，4）两点，动点 P 从 A 出发，在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动，过点P作 PD⊥y 于点 D ，交抛物线于点 C ．设运动时间为 t （秒）．（1）求二次函数
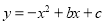的表达式；（2）连接 BC ，当t＝
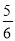时，求△BCP的面积；（3）如图 2，动点 P 从 A 出发时，动点 Q 同时从 O 出发，在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动，当点 P 与 B 重合时，P 、 Q 两点同时停止运动，连接 DQ 、 PQ ，将△DPQ沿直线 PC 折叠到 △DPE ．在运动过程中，设 △DPE 和 △OAB重合部分的面积为 S ，直接写出 S 与 t 的函数关系式及 t 的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某药品说明书上标明药品保存的温度是(10±4) ℃,设该药品合适的保存温度为t ℃,则t的取值范围是.
相关试题
