【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
参考答案:
【答案】对顶角相等;∠2;AB;CD;同位角相等,两直线平行;EF.
【解析】
求出∠1=∠2,根据平行线的判定推出AB∥CD∥EF,根据平行线的性质得出即可.
解:∵∠1=∠3,
又∠2=∠3(对顶角相等),
∴∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
又∵CD∥EF,
∴AB∥EF,
∴∠1=∠4(两直线平行,同位角相等),
故答案为:对顶角相等;∠2;AB;CD;同位角相等,两直线平行;EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明把一副三角板按如图所示叠放在一起,固定三角板
 ,将另一块三角板
,将另一块三角板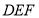 绕公共顶点
绕公共顶点 顺时针旋转(旋转的角度为锐角).若两块三角板有一边平行,则三角板
顺时针旋转(旋转的角度为锐角).若两块三角板有一边平行,则三角板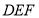 旋转的度数可能是______.
旋转的度数可能是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
-
科目: 来源: 题型:
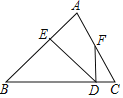
查看答案和解析>>【题目】如图所示,
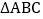 中,
中,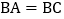 ,点
,点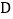 为
为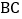 上一点,
上一点,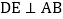 交
交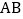 于点
于点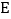 ,
, 交
交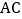 于点
于点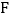 .
.(1)若
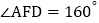 ,则
,则 °;
°; (2)若点
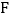 是
是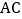 的中点,求证:
的中点,求证: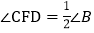 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你根据如图所示的阿宝与仙鹤的对话,解答下列问题:
(1)仙鹤为什么说多边形内角和的度数不可能是
 ;
;(2)若图中仙鹤所提到的外角的度数为
 ,请分别求仙鹤所画的多边形的内角和的度数与边数.
,请分别求仙鹤所画的多边形的内角和的度数与边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.

(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):

(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
相关试题

