【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)、B(3,0)两点,与y轴交于点C(0,3).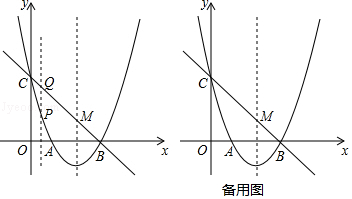
(1)求抛物线的解析式;
(2)设点P是位于直线BC下方的抛物线上一动点,过点P作y轴的平行线交直线BC于点Q,求线段PQ的最大值;
(3)在(2)的条件下,抛物线的对称轴与直线BC交于点M,问是否存在点P,使以M、P、Q为顶点的三角形与△CBO相似?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:把A(1,0),B(3,0),C(0,3)三点代入y=ax2+bx+c,
得 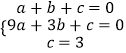 ,解得
,解得 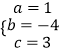 ,
,
则抛物线的解析式为y=x2﹣4x+3;
(2)
解:设直线BC的解析式为y=mx+n,
将点B,C坐标代入y=mx+n,
得 ![]() ,解得
,解得 ![]() ,
,
所以直线BC的解析式为y=﹣x+3.
设P点坐标为(t,t2﹣4t+3),则Q坐标为(t,﹣t+3),
∴PQ=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t=﹣(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,PQ的值最大,最大值为
时,PQ的值最大,最大值为 ![]() ;
;
(3)
解:∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,
∵点M是对称轴与直线BC的交点,
∴将x=2代入y=﹣x+3,得y=﹣2+3=1,即M(2,1).
∵PQ∥y轴,
∴∠PQB=∠OCB,
∴以M,P,Q为顶点的三角形与△OBC相似包含两种情况:△PMQ∽△OBC或△MPQ∽△OBC.
①当△PMQ∽△OBC时,∠QPM=∠COB=90°,即PM⊥PQ,
∴yP=yM=1,
将yP=1代入y=x2﹣4x+3,得x2﹣4x+3=1,
解得x1=2﹣ ![]() ,x2=2+
,x2=2+ ![]() (舍去),
(舍去),
∴此时P(2﹣ ![]() ,1);
,1);
②当△MPQ∽△OBC时,∠QMP=∠COB=90°,即PM⊥BC,
∴kPM= ![]() =1,
=1,
∴可设直线PM的解析式为y=x+d,
将M(2,1)代入y=x+d,
得2+d=1,解得d=﹣1,
∴y=x﹣1,
解方程组 ![]() ,得
,得 ![]() ,
, ![]() (舍去),
(舍去),
∴此时P(1,0).
综上所述,存在点P,使以点M,P,Q为顶点的三角形与△OBC相似,P点坐标为(2﹣ ![]() ,1)或(1,0).
,1)或(1,0).
【解析】(1)把A(1,0),B(3,0),C(0,3)三点代入y=ax2+bx+c,利用待定系数法求得抛物线的解析式;(2)利用待定系数法求得直线BC的解析式为y=﹣x+3.设P点坐标为(t,t2﹣4t+3),则Q坐标为(t,﹣t+3),那么PQ=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,再利用配方法化为顶点式,即可求出PQ的最大值;(3)由PQ∥y轴,得出∠PQB=∠OCB,那么以M,P,Q为顶点的三角形与△OBC相似包含两种情况:①当△PMQ∽△OBC时,PM⊥PQ,yP=yM=1,易求P(2﹣ ![]() ,1);②当△MPQ∽△OBC时,先求直线PM的解析式,再联立PM与抛物线的解析式,求出P(1,0).
,1);②当△MPQ∽△OBC时,先求直线PM的解析式,再联立PM与抛物线的解析式,求出P(1,0).
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图①,△ABC、△AED是两个全等的等腰直角三角形(其顶点B、E重合),∠BAC=∠AED=90°,O为BC的中点,F为AD的中点,连接OF.
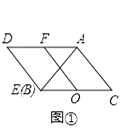
(1)问题发现
①如图①,线段OF与EC的数量关系为;
②将△AED绕点A逆时针旋转45°,如图②,OF与EC的数量关系为;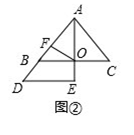
(2)类比延伸
将图①中△AED绕点A逆时针旋转到如图③所示的位置,请判断线段OF与EC的数量关系,并给出证明.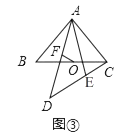
(3)拓展探究
将图①中△AED绕点A逆时针旋转,旋转角为α,0°≤α≤90°,AD=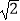 ,△AED在旋转过程中,存在△ACD为直角三角形,请直接写出线段CD的长.
,△AED在旋转过程中,存在△ACD为直角三角形,请直接写出线段CD的长. -
科目: 来源: 题型:
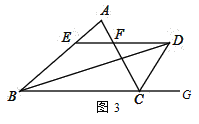
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F
(1) 说明BE=CF的理由
(2) 如果AB=a,AC=b,求AE、BE的长

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点,若一个多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
(1)求出图中格点四边形DEFG对应的S,N,L.
(2)已知格点多边形的面积可表示为S=N+aL+b,其中a,b为常数,若某格点多边形对应的N=82,L=38,求S的值.

-
科目: 来源: 题型:
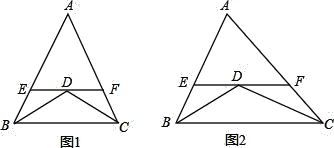
查看答案和解析>>【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
-
科目: 来源: 题型:
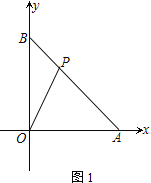
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A、B坐标为(6,0)、(0,6),P为线段AB上的一点
(1) 如图1,若S△AOP=12,求P的坐标
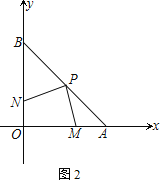
(2) 如图2,若P为AB的中点,点M、N分别是OA、OB边上的动点,点M从顶点A、点N从顶点O同时出发,且它们的速度都为1 cm/s,则在M、N运动的过程中,线段PM、PN之间有何关系?并证明
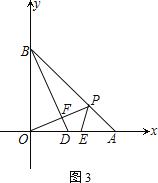
(3) 如图3,若P为线段AB上异于A、B的任意一点,过B点作BD⊥OP,交OP、OA分别与F、D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

相关试题

