【题目】如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y= ![]() (x<0)的图象经过点A,若S△ABO=
(x<0)的图象经过点A,若S△ABO= ![]() ,则k的值为 .
,则k的值为 . 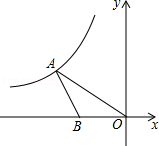
参考答案:
【答案】﹣3 ![]()
【解析】解:过点A作AD⊥x轴于点D,如图所示. 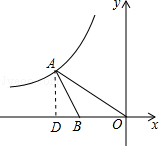
∵∠AOB=30°,AD⊥OD,
∴ ![]() =cot∠AOB=
=cot∠AOB= ![]() ,
,
∵∠AOB=30°,AB=BO,
∴∠AOB=∠BAO=30°,
∴∠ABD=60°,
∴ ![]() =cot∠ABD=
=cot∠ABD= ![]() ,
,
∵OB=OD﹣BD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵S△ABO= ![]() ,
,
∴S△ADO= ![]() |k|=
|k|= ![]() ,
,
∵反比例函数图象在第二象限,
∴k=﹣3 ![]()
故答案为:﹣3 ![]() .
.
过点A作AD⊥x轴于点D,由∠AOB=30°可得出 ![]() =
= ![]() ,再根据BA=BO可得出∠ABD=60°,由此可得出
,再根据BA=BO可得出∠ABD=60°,由此可得出 ![]() =
= ![]() ,根据线段间的关系即可得出线段OB、OD间的比例,结合反比例函数系数k的几何意义以及S△ABO=
,根据线段间的关系即可得出线段OB、OD间的比例,结合反比例函数系数k的几何意义以及S△ABO= ![]() 即可得出结论.
即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
【1】新知学习
⑴梯形的中位线:连接梯形两腰中点的线段叫做梯形的中位线.
⑵梯形的中位线性质:梯形的中位线平行于两底,并且等于两底和的一半.
⑶形如分式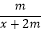 (m为常数,且m>0),若x>0,则
(m为常数,且m>0),若x>0,则 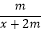 ,并且有下列结论:
,并且有下列结论:
当x 逐渐增大时,分母x+2m逐渐增大,分式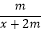 的值逐渐减少并趋于0,但仍大于0.当x 逐渐减少时,分母x+2m逐渐减少,分式
的值逐渐减少并趋于0,但仍大于0.当x 逐渐减少时,分母x+2m逐渐减少,分式 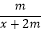 的值逐渐增大并趋于
的值逐渐增大并趋于 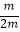 ,即趋于
,即趋于  ,但仍小于
,但仍小于  .
.
【2】问题解决
如图2,已知在梯形ABCD中,AD∥BC,AD<BC,E、F分别是AB、CD的中点.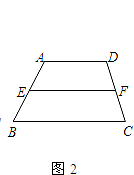
(1)设AD=7,BC=17,求 的值.
的值.
(2)设AD=a(a为正的常数),BC=x,请问:当BC的长不断增大时, 的值能否大于或等于3,试证明你的结论.
的值能否大于或等于3,试证明你的结论.
(3)进一步猜想:任何一个梯形的中位线所分成的两部分图形的面积的比值所在的范围是什么,并说明理由.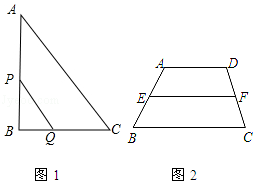
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4…,若∠A=70°,则∠An﹣1AnBn﹣1(n>2)的度数为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.

(1)求证:BE=BF;
(2)若△ABC的面积为70,AB=16,DE=5,则BC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AB=4cm,BC=8cm.点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→D→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了3cm,并沿B→C→D→A的路径匀速运动;点Q保持速度不变,继续沿原路径匀速运动,3s后两点在长方形ABCD某一边上的E点处第二次相遇后停止运动.设点P原来的速度为xcm/s.

(1)点Q的速度为 cm/s(用含x的代数式表示);
(2)求点P原来的速度.
(3)判断E点的位置并求线段DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,∠AOB内有一定点P,且OP=12,在OA上有一点Q,OB上有一点R,若△PQR周长最小,则最小周长是_____

相关试题

