【题目】如图是甲、乙两名射击运动员的10次射击测试成绩的折线统计图.
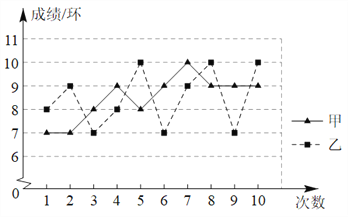
(1)根据折线图把下列表格补充完整;
运动员 | 平均数 | 中位数 | 众数 |
甲 | 8.5 | 9 | |
乙 | 8.5 |
(2)根据上述图表运用所学统计知识对甲、乙两名运动员的射击水平进行评价并说明理由.
参考答案:
【答案】(1)见解析(2)见解析
【解析】分析: (1)把数据从小到大排列,根据中位数和众数的概念求解即可.
(2)答案不唯一,言之有理即可.
(1)补充表格:
运动员 | 平均数 | 中位数 | 众数 |
甲 | 8.5 | 9 | 9 |
乙 | 8.5 | 8.5 | 7和10 |
(2)答案不唯一,可参考的答案如下:
甲选手:和乙选手的平均成绩相同,中位数高于乙,打出9环及以上的次数更多,打出7环的次数较少,说明甲选手相比之下发挥更加稳定;
乙选手:与甲选手平均成绩相同,打出10环次数和7环次数都比甲多,说明乙射击时起伏更大,但也更容易打出10环的成绩.
-
科目: 来源: 题型:
查看答案和解析>>【题目】补全下面的解题过程:
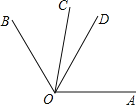
如图,已知OC是∠AOB内部的一条射线,OD是∠AOB的平分线,∠AOC=2∠BOC且∠BOC=40°,求∠COD的度数.
解:因为∠AOC=2∠BOC,∠BOC=40°,所以∠AOC=_____°,所以∠AOB=∠AOC+∠_____=_____°.
因为OD平分∠AOB,所以∠AOD=
 ∠_____=_____°,所以∠COD=∠_____﹣∠AOD=_____°.
∠_____=_____°,所以∠COD=∠_____﹣∠AOD=_____°. -
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角板的两块三角板的三个角度数分别为90°、60°、30°和90°、45°、45°,我们可以用三角板的角拼出一些特殊度数的角.
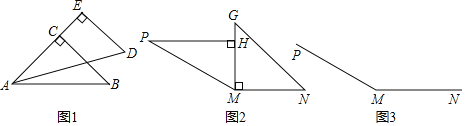
(1)两块三角板按如图1所示拼接,则∠BAD的度数是 °.
(2)小明用两块三角板按图2拼出的∠PMN的度数是 °.
(3)小明想画出图2拼出的∠PMN的角平分线,请你只用一副三角板在图3中帮小明完成画图.(不写画法,保留画图痕迹,标出必要的度数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 过点
过点 ,且与函数
,且与函数 的图象相交于
的图象相交于 两点,与
两点,与 轴、
轴、 轴分别交于点
轴分别交于点 ,如图所示,四边形
,如图所示,四边形 均为矩形,且矩形
均为矩形,且矩形 的面积为
的面积为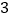 .
.(1)求
 的值;
的值;(2)当点
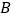 的横坐标为
的横坐标为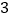 时,求直线
时,求直线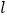 的解析式及线段
的解析式及线段 的长;
的长;(3)如图是小芳同学对线段
 的长度关系的思考示意图.记点
的长度关系的思考示意图.记点 的横坐标为
的横坐标为 ,已知当
,已知当 时,线段
时,线段 的长随
的长随 的增大而减小,请你参考小芳的示意图判断:当
的增大而减小,请你参考小芳的示意图判断:当 时,线段
时,线段 的长随
的长随 的增大而 . (填“增大”、“减小”或“不变”)
的增大而 . (填“增大”、“减小”或“不变”)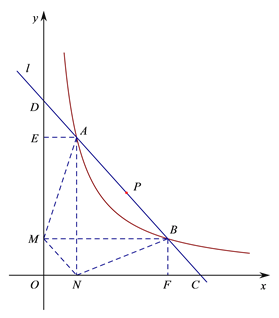
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明对某市出租汽车的计费问题进行研究,他搜集了一些资料,部分信息如下:
收费项目
收费标准
3公里以内收费
13元
基本单价
2.3元/公里
……
……
备注:出租车计价段里程精确到500米;出租汽车收费结算以元为单位,元以下四舍五入。
小明首先简化模型,从简单情形开始研究:①只考虑白天正常行驶(无低速和等候);②行驶路程3公里以上时,计价器每500米计价1次,且每1公里中前500米计价1.2元,后500米计价1.1元.
下面是小明的探究过程,请补充完整:
记一次运营出租车行驶的里程数为
 (单位:公里),相应的实付车费为
(单位:公里),相应的实付车费为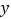 (单位:元).
(单位:元).(1)下表是y随x的变化情况
行驶里程数x
0
0<x<3.5
3.5≤x<4
4≤x<4.5
4.5≤x<5
5≤x<5.5
…
实付车费y
0
13
14
15
…
(2)在平面直角坐标系
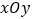 中,画出当
中,画出当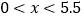 时
时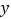 随
随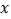 变化的函数图象;
变化的函数图象;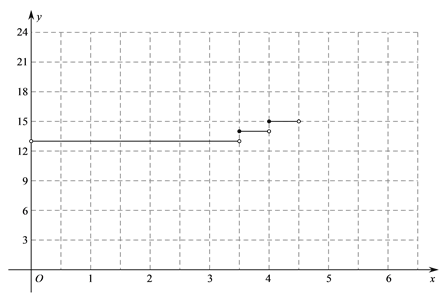
(3)一次运营行驶
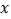 公里(
公里( )的平均单价记为
)的平均单价记为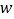 (单位:元/公里),其中
(单位:元/公里),其中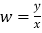 .
.①当
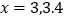 和
和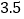 时,平均单价依次为
时,平均单价依次为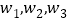 ,则
,则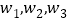 的大小关系是____________;(用“<”连接)
的大小关系是____________;(用“<”连接)②若一次运营行驶
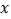 公里的平均单价
公里的平均单价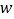 不大于行驶任意
不大于行驶任意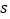 (
(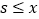 )公里的平均单价
)公里的平均单价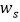 ,则称这次行驶的里程数为幸运里程数.请在上图中
,则称这次行驶的里程数为幸运里程数.请在上图中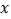 轴上表示出
轴上表示出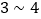 (不包括端点)之间的幸运里程数
(不包括端点)之间的幸运里程数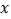 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为充分利用我县红色旅游资源和汀江绿道观光资源,发展我县旅游经济、绿色经济.某旅游公司推出年卡优惠活动,其中三类年卡及相应费用如表所示:
年卡类别
畅游版
优惠版
乐享版
年卡费用(元)
130
100
60
(1)某代售点在某日卖出上述三种年卡共30张,其中乐享版年卡比畅游版年卡多卖出5张,30张年卡费用总计2750元.求该代售点当日卖出优惠版年卡多少张?
(2)另一家代售点在某日卖出这三类年卡各若干张(三类年卡卖出张数均为正整数),卖出的年卡费用总计3100元,其中卖出的畅游版和乐享版年卡张数相同,问该代售点当日卖出三类年卡共多少张?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.若∠AOD=120°,AC=4,则CD的大小为( )
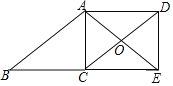
A.8B.4
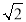 C.8
C.8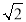 D.6
D.6
相关试题

