【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求![]() 的值.
的值.

参考答案:
【答案】(1)(2)见解析;(3)![]()
【解析】试题分析:(1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=ABAD;
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=![]() AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,即可得到结论.
试题解析:(1)证明:∵AC平分∠DAB,∴∠DAC=∠CAB.∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,∴AD:AC=AC:AB,∴AC2=ABAD;
(2)证明:∵E为AB的中点,∴CE=![]() AB=AE,∴∠EAC=∠ECA.∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥A D;
AB=AE,∴∠EAC=∠ECA.∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥A D;
(3)解:∵CE∥AD,∴△AFD∽△CFE,∴AD:CE=AF:CF.∵CE= ![]() AB,∴CE=
AB,∴CE=![]() ×6=3.∵AD=4,∴
×6=3.∵AD=4,∴![]() ,∴
,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①若a,b互为相反数,则
 =-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为
=-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为 分.其中正确的为____(填序号).
分.其中正确的为____(填序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A, B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).

(1)填空:从图可知,每个小长方形较长的一边长是_________cm (用含y的代数式表示).
(2)分别求出阴影 A,B的面积,并计算阴影 A,B的面积差?(用含x,y的式子表示)
(3)当y=10时,阴影 A与阴影 B的面积差会随着x的变化而变化吗?请你作出判断,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是
是 的函数,自变量
的函数,自变量 的取值范围为
的取值范围为 ,下表是
,下表是 与
与 的几组对应值
的几组对应值
0
1
2
3
3.5
4
4.5
…

1
2
3
4
3
2
1
…
小明根据学习函数的经验,利用上述表格所反映出的
 与
与 之间的变化规律,对该函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
之间的变化规律,对该函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整:(1)如图,在平面直角坐标系中,指出了以上表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象.

(2)根据画出的函数图象填空.
①该函数图象与
 轴的交点坐标为_____.
轴的交点坐标为_____.②直接写出该函数的一条性质.
-
科目: 来源: 题型:
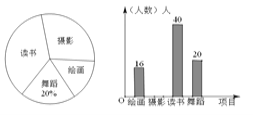
查看答案和解析>>【题目】某学校为了丰富学生业余生活,决定组建绘画、摄影、读书和舞蹈兴趣活动小组,为了解学生最喜欢哪一种活动的人数,随机抽取了部分学生进行调查(每位学生必选且只能选一项),并将调查结果绘制成了两幅不完整的统计图,请你根据统计图上提供的信息回答下列问题:
(1)这次被调查的学生共有多少人,并将条形统计图补充完整;
(2)在扇形统计图中,求出最喜欢“读书”所对应的圆心角度数;
(3)若该校共有学生2000人,请你估计该校最喜欢读书活动的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小芳去商店购买甲、乙两种商品. 现有如下信息:
信息1:甲、乙两种商品的进货单价之和是5元,按零售单价购买甲商品3件和乙商品2件,共付了19元;
信息2:甲商品零售单价比甲进货单价多1元,乙商品零售单价比乙进货单价的2倍少1元.
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)若小芳准备用不超过400元钱购买100件甲、乙两种商品,其中甲种商品至少购买多少件?
相关试题

