【题目】如图 1,在平面直角坐标系中,直线l1:yx5与x轴,y轴分别交于A.B两点.直线l2:y4xb与l1交于点 D(-3,8)且与x轴,y轴分别交于C、E.
(1)求出点A坐标,直线l2的解析式;
(2)如图2,点P为线段AD上一点(不含端点),连接CP,一动点Q从C出发,沿线段CP 以每秒1个单位的速度运动到点P,再沿着线段PD以每秒![]() 个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
(3)如图3,平面直角坐标系中有一点G(m,2),使得SCEGSCEB,求点G的坐标.

参考答案:
【答案】(1)A(5,0),y4x-4;
(2)8秒, P(-1,6);
(3)![]() .
.
【解析】
(1)根据l1解析式,y=0即可求出点A坐标,将D点代入l2解析式并解方程,即可求出l2解析式
(2)根据OA=OB可知![]() ABO和
ABO和![]() DPQ都为等腰直角三角形,根据路程和速度,可得点Q在整个运动过程中所用的时间为
DPQ都为等腰直角三角形,根据路程和速度,可得点Q在整个运动过程中所用的时间为![]() ,当C,P,Q三点共线时,t有最小值,根据矩形的判定和性质可以求出P和Q的坐标以及最小时间.
,当C,P,Q三点共线时,t有最小值,根据矩形的判定和性质可以求出P和Q的坐标以及最小时间.
(3)用面积法![]() ,用含m的表达式求出
,用含m的表达式求出![]() ,根据SCEGSCEB可以求出G点坐标.
,根据SCEGSCEB可以求出G点坐标.
(1)直线l1:yx5,令y=0,则x=5,
故A(5,0).
将点D(-3,8)代入l2:y4xb,
解得b=-4,
则直线l2的解析式为y4x-4.
∴点A坐标为A(5,0),直线l2的解析式为y4x-4.
(2)如图所示,过P点做y轴平行线PQ,做D点做x轴平行线DQ,PQ与DQ相交于点Q,可知![]() DPQ为等腰直角三角形,
DPQ为等腰直角三角形,![]() .
.

依题意有![]()
当C,P,Q三点共线时,t有最小值,此时![]()
故点Q在整个运功过程中所用的最少时间是8秒,此时点P的坐标为(-1,6).
(3)如图过G做x轴平行线,交直线CD于点H,过C点做CJ⊥HG.

根据l2的解析式,可得点H(![]() ),E(0,-4),C(-1,0)
),E(0,-4),C(-1,0)
根据l1的解析式,可得点A(5,0),B(0,5)
则GH=![]()
![]()
又SCEGSCEB
所以![]() ,解得
,解得![]()
故![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
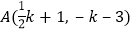 、
、 在反比例函数
在反比例函数 上,作等腰直角三角形
上,作等腰直角三角形 ,点
,点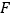 为斜边
为斜边 的中点,连
的中点,连 并延长交
并延长交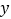 轴于点
轴于点 .
.
 求反比例函数的解析式;
求反比例函数的解析式; 的面积是多少?
的面积是多少? 若点
若点 在直线
在直线 上,请求出直线
上,请求出直线 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明为校合唱队购买某种服装时,商店经理给出了如下优惠条件:如果一次性购买不超过
 件,单价为
件,单价为 元;如果一次性购买多于
元;如果一次性购买多于 件,那么每增加
件,那么每增加 件,购买的所有服装的单价降低
件,购买的所有服装的单价降低 元,但单价不得低于
元,但单价不得低于 元.按此优惠条件,小明一次性购买这种服装
元.按此优惠条件,小明一次性购买这种服装 (
( 为正整数)件,支付
为正整数)件,支付 元.
元. 当
当 时,小明购买的这种服装的单价为________元;
时,小明购买的这种服装的单价为________元; 写出
写出 关于
关于 的函数表达式,并给出自变量
的函数表达式,并给出自变量 的取值范围;
的取值范围; 小明一次性购买这种服装付了
小明一次性购买这种服装付了 元,请问他购买了多少件这种服装?
元,请问他购买了多少件这种服装? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=2,AC=
 ,AD是△ABC的高,且 BD=1.
,AD是△ABC的高,且 BD=1.(1)求 BC的长.
(2)E是边AC上的一点,作射线BE,分别过点A、C 作 AF⊥BE于点 F,CG⊥BE于点 G,如图2,若 BE=
 ,求 AF与 CG的和.
,求 AF与 CG的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①图象经过点(1,﹣3);②关于x的方程kx+b=0的解为x=2;③关于x的方程kx+b=3的解为x=0;④当x>2时,y<0.其中正确的是( )

A.①②③B.①③④C.②③④D.①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(﹣3,0),点B(0,4),点C在x轴正半轴上,若△ABC是等腰三角形,那么所有满足条件的点C的坐标是_____.
相关试题

