【题目】在平面直角坐标系中,点A(﹣3,0),点B(0,4),点C在x轴正半轴上,若△ABC是等腰三角形,那么所有满足条件的点C的坐标是_____.
参考答案:
【答案】(![]() ,0)或(2,0)或(3,0)
,0)或(2,0)或(3,0)
【解析】
根据勾股定理求得AB的长,然后分三种情况讨论得到点C的坐标.
∵点A(﹣3,0),点B(0,4),
∴OA=3,OB=4,
∴AB=![]() =5,
=5,
若△ABC是等腰三角形,
①当AC=BC,则点C在AB的垂直平分线上,
∵BC2﹣OC2=42,
∴(3+OC)2﹣OC2=16,
解得:OC=![]() ,
,
∴点C的坐标是(![]() ,0),
,0),
②当AB=AC=5时,
则OC=2,
∴点C的坐标是(2,0),
③当AB=BC=5时,OC=OA=3,
∴点C的坐标是(3,0),
综上所述,点C的坐标是(![]() ,0)或(2,0)或(3,0).
,0)或(2,0)或(3,0).
故答案为:(![]() ,0)或(2,0)或(3,0).
,0)或(2,0)或(3,0).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,在平面直角坐标系中,直线l1:yx5与x轴,y轴分别交于A.B两点.直线l2:y4xb与l1交于点 D(-3,8)且与x轴,y轴分别交于C、E.
(1)求出点A坐标,直线l2的解析式;
(2)如图2,点P为线段AD上一点(不含端点),连接CP,一动点Q从C出发,沿线段CP 以每秒1个单位的速度运动到点P,再沿着线段PD以每秒
 个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;(3)如图3,平面直角坐标系中有一点G(m,2),使得SCEGSCEB,求点G的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①图象经过点(1,﹣3);②关于x的方程kx+b=0的解为x=2;③关于x的方程kx+b=3的解为x=0;④当x>2时,y<0.其中正确的是( )

A.①②③B.①③④C.②③④D.①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
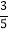 时,求AB的长.
时,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx过点B(1,﹣3),对称轴是直线x=2,且抛物线与x轴的正半轴交于点A.
(1)求抛物线的解析式,并根据图象直接写出当y≤0时,自变量x的取值范图;
(2)在第二象限内的抛物线上有一点P,当PA⊥BA时,求△PAB的面积.

相关试题

