【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=x2-4x+3.(2)当m=![]() 时,四边形AOPE面积最大,最大值为
时,四边形AOPE面积最大,最大值为![]() .(3)P点的坐标为 :P1(
.(3)P点的坐标为 :P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ).
).
【解析】
(1)利用对称性可得点D的坐标,利用交点式可得抛物线的解析式;
(2)设P(m,m2-4m+3),根据OE的解析式表示点G的坐标,表示PG的长,根据面积和可得四边形AOPE的面积,利用配方法可得其最大值;
(3)存在四种情况:
如图3,作辅助线,构建全等三角形,证明△OMP≌△PNF,根据OM=PN列方程可得点P的坐标;同理可得其他图形中点P的坐标.
(1)如图1,设抛物线与x轴的另一个交点为D,
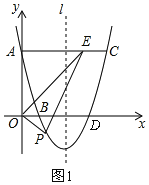
由对称性得:D(3,0),
设抛物线的解析式为:y=a(x-1)(x-3),
把A(0,3)代入得:3=3a,
a=1,
∴抛物线的解析式;y=x2-4x+3;
(2)如图2,设P(m,m2-4m+3),
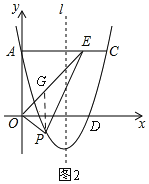
∵OE平分∠AOB,∠AOB=90°,
∴∠AOE=45°,
∴△AOE是等腰直角三角形,
∴AE=OA=3,
∴E(3,3),
易得OE的解析式为:y=x,
过P作PG∥y轴,交OE于点G,
∴G(m,m),
∴PG=m-(m2-4m+3)=-m2+5m-3,
∴S四边形AOPE=S△AOE+S△POE,
=![]() ×3×3+
×3×3+![]() PGAE,
PGAE,
=![]() +
+![]() ×3×(-m2+5m-3),
×3×(-m2+5m-3),
=-![]() m2+
m2+![]() m,
m,
=![]() (m-
(m-![]() )2+
)2+![]() ,
,
∵-![]() <0,
<0,
∴当m=![]() 时,S有最大值是
时,S有最大值是![]() ;
;
(3)如图3,过P作MN⊥y轴,交y轴于M,交l于N,
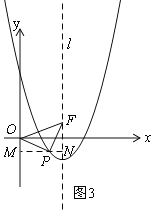
∵△OPF是等腰直角三角形,且OP=PF,
易得△OMP≌△PNF,
∴OM=PN,
∵P(m,m2-4m+3),
则-m2+4m-3=2-m,
解得:m=![]() 或
或![]() ,
,
∴P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
如图4,过P作MN⊥x轴于N,过F作FM⊥MN于M,
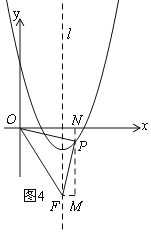
同理得△ONP≌△PMF,
∴PN=FM,
则-m2+4m-3=m-2,
解得:x=![]() 或
或![]() ;
;
P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
综上所述,点P的坐标是:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
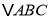 中,
中,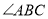 和
和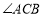 的平分线相交于点
的平分线相交于点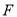 ,过
,过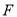 作
作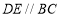 ,交
,交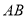 于点
于点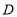 ,交
,交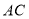 于点
于点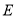 .若
.若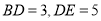 ,则线段
,则线段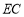 的长为______.
的长为______.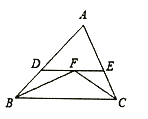
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=
 ,反比例函数y=
,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.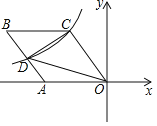
-
科目: 来源: 题型:
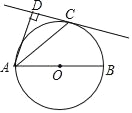
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O上,AD⊥CD于点D,且AC平分∠DAB,求证:
(1)直线DC是⊙O的切线;
(2)AC2=2ADAO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形
 中,
中, ,点
,点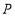 从
从 点出发,沿折线
点出发,沿折线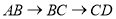 运动,到点
运动,到点 时停止,已知
时停止,已知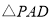 的面积
的面积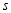 与点
与点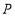 运动的路程
运动的路程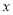 的函数图象如图②所示,则点
的函数图象如图②所示,则点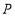 从开始到停止运动的总路程为________.
从开始到停止运动的总路程为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并回答问题.事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方,这个结论就是著名的勾股定理.请利用这个结论,完成下面活动:
 一个直角三角形的两条直角边分别为
一个直角三角形的两条直角边分别为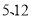 ,那么这个直角三角形斜边长为____;
,那么这个直角三角形斜边长为____; 如图①,
如图①,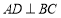 于
于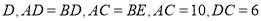 ,求
,求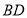 的长度;
的长度; 如图②,点
如图②,点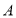 在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数
在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数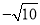 的
的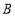 点(保留痕迹).
点(保留痕迹). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+b.
(1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.
相关试题

