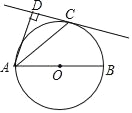
【题目】如图,AB为⊙O的直径,点C在⊙O上,AD⊥CD于点D,且AC平分∠DAB,求证:
(1)直线DC是⊙O的切线;
(2)AC2=2ADAO.
参考答案:
【答案】(1)证明见解析.(2)证明见解析.
【解析】(1)连接OC,由OA=OC、AC平分∠DAB知∠OAC=∠OCA=∠DAC,据此知OC∥AD,根据AD⊥DC即可得证;
(2)连接BC,证△DAC∽△CAB即可得.
(1)如图,连接OC,
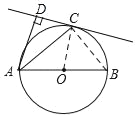
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠OAC=∠DAC,
∴∠DAC=∠OCA,
∴OC∥AD,
又∵AD⊥CD,
∴OC⊥DC,
∴DC是⊙O的切线;
(2)连接BC,
∵AB为⊙O的直径,
∴AB=2AO,∠ACB=90°,
∵AD⊥DC,
∴∠ADC=∠ACB=90°,
又∵∠DAC=∠CAB,
∴△DAC∽△CAB,
∴![]() ,即AC2=ABAD,
,即AC2=ABAD,
∵AB=2AO,
∴AC2=2ADAO.
-
科目: 来源: 题型:
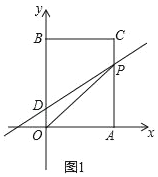
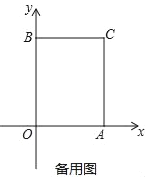
查看答案和解析>>【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
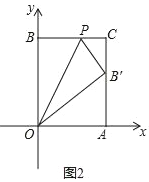
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
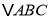 中,
中,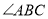 和
和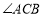 的平分线相交于点
的平分线相交于点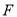 ,过
,过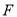 作
作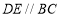 ,交
,交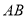 于点
于点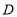 ,交
,交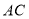 于点
于点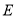 .若
.若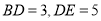 ,则线段
,则线段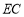 的长为______.
的长为______.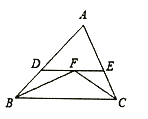
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=
 ,反比例函数y=
,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.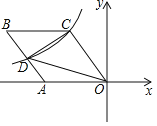
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形
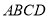 中,
中, ,点
,点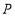 从
从 点出发,沿折线
点出发,沿折线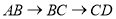 运动,到点
运动,到点 时停止,已知
时停止,已知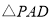 的面积
的面积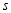 与点
与点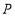 运动的路程
运动的路程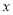 的函数图象如图②所示,则点
的函数图象如图②所示,则点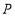 从开始到停止运动的总路程为________.
从开始到停止运动的总路程为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并回答问题.事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方,这个结论就是著名的勾股定理.请利用这个结论,完成下面活动:
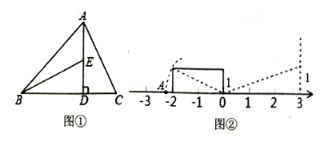
 一个直角三角形的两条直角边分别为
一个直角三角形的两条直角边分别为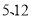 ,那么这个直角三角形斜边长为____;
,那么这个直角三角形斜边长为____;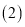 如图①,
如图①,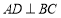 于
于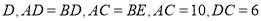 ,求
,求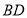 的长度;
的长度; 如图②,点
如图②,点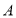 在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数
在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数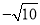 的
的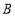 点(保留痕迹).
点(保留痕迹).
相关试题

