【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过
,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,则线段
,则线段![]() 的长为______.
的长为______.
参考答案:
【答案】2
【解析】
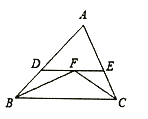
根据角平分线的定义可得∠DBF=∠FBC,∠ECF=∠FCB,由平行线的性质可得∠DFB=∠FBC,∠EFC=∠FCB,等量代换可得∠DFB=∠DBF,∠EFC=∠ECF,根据等角对等边可得到DF=DB,EF=EC,再由ED=DF+EF结合已知即可求得答案.
∵BF、CF分别是∠ABC和∠ACB的角平分线,
∴∠DBF=∠FBC,∠ECF=∠FCB,
∵DE∥ BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∴∠DFB=∠DBF,∠EFC=∠ECF,
∴DF=DB,EF=EC,
∵ED=DF+EF,![]() ,
,
∴EF=2,
∴EC=2
故答案为:2
-
科目: 来源: 题型:
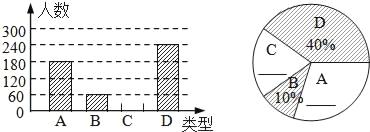
查看答案和解析>>【题目】“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗.某食品厂为了解市民对去年销量较好的肉馅(A)、豆沙馅 (B)、菜馅(C)、三丁馅 (D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:
(1)本次参加抽样调查的居民人数是 人;
(2)将图 ①②补充完整;( 直接补填在图中)
(3)求图②中表示“A”的圆心角的度数;
(4)若居民区有8000人,请估计爱吃D汤圆的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OB,AB⊥x轴于C,点A(
 ,1)在反比例函数y=
,1)在反比例函数y= 的图象上.
的图象上.
(1)求反比例函数y=
 的表达式;
的表达式; (2)在x轴上存在一点P,使S△AOP=
 S△AOB, 求点P的坐标.
S△AOB, 求点P的坐标. -
科目: 来源: 题型:
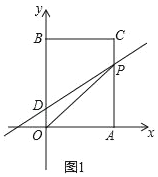
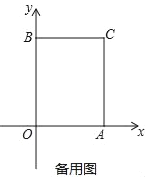
查看答案和解析>>【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
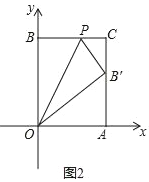
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=
 ,反比例函数y=
,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.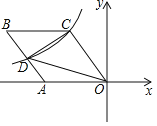
-
科目: 来源: 题型:
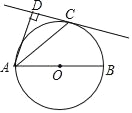
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O上,AD⊥CD于点D,且AC平分∠DAB,求证:
(1)直线DC是⊙O的切线;
(2)AC2=2ADAO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
相关试题

