【题目】在直角坐标系中,已知点A、B的坐标是(a,0)(b,0),a,b满足方程组![]() ,C为y轴正半轴上一点,且S△ABC=6.
,C为y轴正半轴上一点,且S△ABC=6.
(1)求A、B、C三点的坐标;
(2)是否存在点P(t,t),使S△PAB=![]() S△ABC?若存在,请求出P点坐标;若不存在,请说明理由;
S△ABC?若存在,请求出P点坐标;若不存在,请说明理由;
(3)若点C沿y轴负半轴方向以每秒1个单位长度平移至点D,当运动时间t为多少秒时,四边形ABCD的面积S为15个平方单位?求出此时点D的坐标.

参考答案:
【答案】(1)A(-3,0),B(1,0),C(0,3);(2)存在P(1,1)或(-1,-1);(3)D(0,-4.5)
【解析】
(1)解出方程组即可得到时点A,B的坐标,利用S△ABC=6,求出点C的坐标;
(2)利用S△PAB=![]() S△ABC求出点P的坐标即可;
S△ABC求出点P的坐标即可;
(3)设D(0,m),由S四边形ABCD=S△ABC+S△ABD =15求m值即可.
(1)由方程组![]() ,解得
,解得![]() ,
,
∴A(-3,0),B(1,0),
∵c为y轴正半轴上一点,且S△ABC=6,
∴![]() ABOC=6,解得:OC=3,
ABOC=6,解得:OC=3,
∴C(0,3);
(2)存在.
理由:∵P(t,t),且S△PAB=![]() S△ABC,
S△ABC,
∴![]() ×4×|t|=
×4×|t|=![]() ×6,
×6,
解得t=±1,
∴P(1,1)或(-1,-1);
(3)设D(0,m),
由S四边形ABCD=S△ABC+S△ABD=6+S△ABD=15,
∴S△ABD=9,
∴![]() ×4×(-m)=9,
×4×(-m)=9,
解得m=-4,5,
∴D(0,-4.5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①若式子
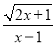 有意义,则
有意义,则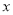 的取值范围是
的取值范围是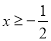 ;②正多边形的的一个内角是140°,则这个多边形是正九边形;③甲、乙两人进行射击测试,每人次射击成绩的平均数都是8.8环,方差分别是
;②正多边形的的一个内角是140°,则这个多边形是正九边形;③甲、乙两人进行射击测试,每人次射击成绩的平均数都是8.8环,方差分别是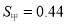 ,
,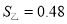 ,则射击成绩最稳定的是乙;④若
,则射击成绩最稳定的是乙;④若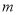 是方程
是方程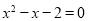 的一个实数根,则
的一个实数根,则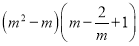 的值是4.其中正确的有( )个
的值是4.其中正确的有( )个A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为8的等边
 置于平面直角坐标系中,点
置于平面直角坐标系中,点 在
在 轴正半轴上,过点
轴正半轴上,过点 作
作 于点
于点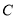 ,将
,将 绕着原点
绕着原点 逆时针旋转
逆时针旋转 得到
得到 ,这时,点
,这时,点 恰好落在
恰好落在 轴上.若动点
轴上.若动点 从原点
从原点 出发,沿线段
出发,沿线段 向终点
向终点 运动,动点
运动,动点 从点
从点 出发,沿线段
出发,沿线段 向终点
向终点 运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为
运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为 秒.
秒.(1)请直接写出点
 、点
、点 的坐标;
的坐标;(2)当
 的面积为
的面积为 时,求
时,求 的值;
的值;(3)设
 与
与 相交于点
相交于点 ,当
,当 为何值时,
为何值时,  与
与 相似?
相似?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个一元二次方程
 ,
, ,其中,
,其中,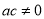 ,
, ,下列四个结论中错误的是( )
,下列四个结论中错误的是( )A.如果方程
 有两个不相等的实数根,那么方程
有两个不相等的实数根,那么方程 也有两个不相等的实数
也有两个不相等的实数B.如果4是方程
 的一个根,那么
的一个根,那么 是方程
是方程 的另一个根
的另一个根C.如果方程
 有两根符号相同,那么方程
有两根符号相同,那么方程 的两符号也相同
的两符号也相同D.如果方程
 和方程
和方程 有一个相同的根,那么这个根必是
有一个相同的根,那么这个根必是
-
科目: 来源: 题型:
查看答案和解析>>【题目】若自然数
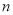 使得三个数的加法运算“
使得三个数的加法运算“ ”产生进位现象,则称
”产生进位现象,则称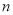 为“连加进位数”.例如:2不是“连加进位数”,因为
为“连加进位数”.例如:2不是“连加进位数”,因为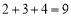 不产生进位现象;4是“连加进位数”,因为
不产生进位现象;4是“连加进位数”,因为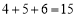 产生进位现象;51是“连加进位数”,因为
产生进位现象;51是“连加进位数”,因为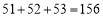 产生进位现象.如果从0,1,2,…,99这100个自然数中任取一个数,取到“连加进位数”的个数有( )个
产生进位现象.如果从0,1,2,…,99这100个自然数中任取一个数,取到“连加进位数”的个数有( )个A.88B.89C.90D.91
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你用实例解释下列代数式的意义:
(1)5a+10b;
(2)3x;
(3)
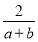 ;
; (4)
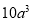 ;
;(5)(1-8%)x;
(6)
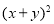 ;
;(7)
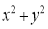 ;
;(8)
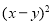 ;
;(9)
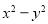 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明将连续的奇数1,3,5,7,9,…,排成如图所示的数阵,用一个矩形框框住其中的9个数,如图所示.
(1)矩形阴影框中的9个数的和与中间一个数存在怎样的关系?(直接写出笞案)
(2)若将矩形框上下左右移动,这个关系还成立吗?为什么?

相关试题

