【题目】如图,将边长为8的等边![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 在
在![]() 轴正半轴上,过点
轴正半轴上,过点![]() 作
作![]() 于点
于点![]() ,将
,将![]() 绕着原点
绕着原点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,这时,点
,这时,点![]() 恰好落在
恰好落在![]() 轴上.若动点
轴上.若动点![]() 从原点
从原点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为
运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为![]() 秒.
秒.
(1)请直接写出点![]() 、点
、点![]() 的坐标;
的坐标;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 的值;
的值;
(3)设![]() 与
与![]() 相交于点
相交于点![]() ,当
,当![]() 为何值时,
为何值时, ![]() 与
与![]() 相似?
相似?

参考答案:
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 秒或
秒或![]() 秒时,
秒时, ![]() 与
与![]() 相似.
相似.
【解析】试题分析:(1)根据等边三角形的性质可直接得出A点坐标;再由OC⊥AB可得出OC的长,根据图形旋转不变性的性质可得出OD的长,进而得出D点坐标;
(2)过点E作EG⊥OD于点G,根据等边三角形的性质可知OC平分∠AOB,再根据锐角三角函数的定义求出EG的长,S△OEF=![]() OFEG,OF=OD﹣DF=
OFEG,OF=OD﹣DF=![]() ﹣t即可得出t的值;
﹣t即可得出t的值;
(3)由于∠BOD=∠FOP,△OPF∽△ODB和△OPF∽△OBD两种情况进行讨论.
试题解析:解:(1)∵等边△AOB的边长为8,点A在x轴正半轴上,∴A(8,0),∵OC⊥AB,∴∠AOC=30°,∴OC=OAcos30°=8×![]() =
=![]() ,∵△OAC旋转后OC与OD重合,∴D(0,
,∵△OAC旋转后OC与OD重合,∴D(0, ![]() );
);
(2)过点E作EG⊥OD于点G,如图①所示:
∵△OAB为等边三角形,OC⊥AB,∴OC平分∠AOB,∴∠AOC=30°,∴∠EOG=90°﹣30°=60°,∴EG=OEsin∠EOG=![]() t,又∵S△OEF=
t,又∵S△OEF=![]() OFEG,OF=OD﹣DF=
OFEG,OF=OD﹣DF=![]() ﹣t,由题意可得:
﹣t,由题意可得: ![]() (
(![]() ﹣t)
﹣t)![]() t=
t=![]() ,解得t=
,解得t=![]() ±3;
±3;
(3)因为∠BOD=∠FOP,所以应分两种情况讨论:
①当∠FPO=∠BDO=90°时,如图②,∵△OPF∽△ODB,此时OE=OF,∴t=![]() ﹣t,解得:t=
﹣t,解得:t=![]() ;
;
②当∠OFP=∠ODB=90°时,如图③,∵△OPF∽△OBD,∴OF=![]() OE,即(
OE,即(![]() ﹣t)=
﹣t)=![]() t,解得:t=
t,解得:t=![]() .
.
综上所述,当t=![]() 秒或t=
秒或t=![]() 秒时,△OPF与△OBD相似.
秒时,△OPF与△OBD相似.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“你今天光盘了吗?”这是国家倡导厉行节约,反对浪费以来的时尚流行语,某校团委随机抽取部分了学生,对他们是否了解关于“光盘行动”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.团委根据调查的数据进行整理,绘制了尚不完整的统计图如下,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题:

(1)求本次活动共调查了多少名学生?
(2)请补全图2,并求出图1中,B区域的圆心角度数;
(3)若该校有2400名学生,请估算该校不是了解很多的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现计划把1240吨甲种货物和880吨乙种货物用一列火车运往某地,已知这列火车挂有A、B两种不同规格的货车车厢共40节,使用A型车厢每节费用为6000元,B型车厢每节费用8000元.如果每节A型车厢最多可装35吨甲种货物和15吨乙种货物,每节B型车厢最多可装25吨甲种货物和35吨乙种货物;
(1)那么共有哪几种安排车厢的方案?
(2)在上述方案中,哪种方案运费最省、最少运费为多少元?
(3)在(1)问下,若两种货物全部售出,且每吨货物售出获利200元,除去运费获
利154000元,问:在这种情况下是按哪种方案安排车厢的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①若式子
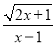 有意义,则
有意义,则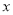 的取值范围是
的取值范围是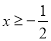 ;②正多边形的的一个内角是140°,则这个多边形是正九边形;③甲、乙两人进行射击测试,每人次射击成绩的平均数都是8.8环,方差分别是
;②正多边形的的一个内角是140°,则这个多边形是正九边形;③甲、乙两人进行射击测试,每人次射击成绩的平均数都是8.8环,方差分别是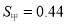 ,
,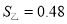 ,则射击成绩最稳定的是乙;④若
,则射击成绩最稳定的是乙;④若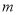 是方程
是方程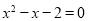 的一个实数根,则
的一个实数根,则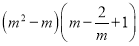 的值是4.其中正确的有( )个
的值是4.其中正确的有( )个A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个一元二次方程
 ,
, ,其中,
,其中,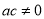 ,
, ,下列四个结论中错误的是( )
,下列四个结论中错误的是( )A.如果方程
 有两个不相等的实数根,那么方程
有两个不相等的实数根,那么方程 也有两个不相等的实数
也有两个不相等的实数B.如果4是方程
 的一个根,那么
的一个根,那么 是方程
是方程 的另一个根
的另一个根C.如果方程
 有两根符号相同,那么方程
有两根符号相同,那么方程 的两符号也相同
的两符号也相同D.如果方程
 和方程
和方程 有一个相同的根,那么这个根必是
有一个相同的根,那么这个根必是
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知点A、B的坐标是(a,0)(b,0),a,b满足方程组
 ,C为y轴正半轴上一点,且S△ABC=6.
,C为y轴正半轴上一点,且S△ABC=6.(1)求A、B、C三点的坐标;
(2)是否存在点P(t,t),使S△PAB=
 S△ABC?若存在,请求出P点坐标;若不存在,请说明理由;
S△ABC?若存在,请求出P点坐标;若不存在,请说明理由;(3)若点C沿y轴负半轴方向以每秒1个单位长度平移至点D,当运动时间t为多少秒时,四边形ABCD的面积S为15个平方单位?求出此时点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若自然数
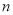 使得三个数的加法运算“
使得三个数的加法运算“ ”产生进位现象,则称
”产生进位现象,则称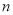 为“连加进位数”.例如:2不是“连加进位数”,因为
为“连加进位数”.例如:2不是“连加进位数”,因为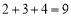 不产生进位现象;4是“连加进位数”,因为
不产生进位现象;4是“连加进位数”,因为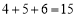 产生进位现象;51是“连加进位数”,因为
产生进位现象;51是“连加进位数”,因为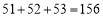 产生进位现象.如果从0,1,2,…,99这100个自然数中任取一个数,取到“连加进位数”的个数有( )个
产生进位现象.如果从0,1,2,…,99这100个自然数中任取一个数,取到“连加进位数”的个数有( )个A.88B.89C.90D.91
相关试题

