【题目】阅读下面材料:小聪遇到这样一个问题: 如图1,![]() ,请画一个
,请画一个![]() ,使
,使![]() 与
与![]() 互补.
互补.

小聪是这样思考的:首先通过分析明确射线![]() 在
在![]() 的外部,画出示意图,如图2所示:然后通过构造平角找到
的外部,画出示意图,如图2所示:然后通过构造平角找到![]() 的补角
的补角![]() ,
,

如图3所示:进而分析要使![]() 与
与![]() 互补,则需
互补,则需![]() .
.

因此,小聪找到了解决问题的方法:反向延长射线![]() 得到射线
得到射线![]() ,利用量角器画出
,利用量角器画出![]() 的平分线
的平分线![]() ,这样就得到了
,这样就得到了![]() 与
与![]() 互补
互补
(1)小聪根据自己的画法写出了己知和求证,请你完成证明.已知:如图3,点![]() 在直线
在直线![]() 上,射线
上,射线![]() 平分
平分![]() .求证:
.求证: ![]() 与
与![]() 互补. .
互补. .

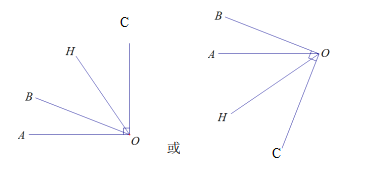
(2)参考小聪的画法,请在下图中画出--个![]() ,使
,使![]() 与
与![]() 互余.(保留画图痕迹)
互余.(保留画图痕迹)

(3)已知![]() 和
和![]() 互余,射线
互余,射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .若
.若![]() ,直接写出锐角
,直接写出锐角![]() 的度数是 .
的度数是 .
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() 或
或![]()
【解析】
(1)根据邻补角的定义得出![]() ,再根据角平分线的定义可得
,再根据角平分线的定义可得![]() ,从而得出
,从而得出![]() 与
与![]() 互补.
互补.
(2)先构造直角,画![]() 或
或![]() ,再利用量角器画出
,再利用量角器画出![]() 或
或![]() 的平分线
的平分线![]() ,即可得出
,即可得出![]() 与
与![]() 互余
互余
(3)先分PF在PQ的右侧和左侧,画出图形,再根据角平分线的性质和角的和差即可得出结论
解:(1)证明:![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() .
.
即![]() .
.
![]() .
.
![]() 平分
平分![]() ,
,
![]() .
.
![]()
![]() 与
与![]() 互补.
互补.
(2) 画![]() 或
或![]() ,再分别画出
,再分别画出![]() 或
或![]() 的平分线
的平分线![]()
如图所示
(3) 当PF在PQ的右侧时,根据题意画出图形如图
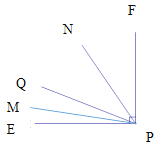
∵射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .
.
∴![]() ,
,![]()
∴![]()
∵![]() 和
和![]() 互余,
互余,
∴![]()
∴![]()
当PF在PQ的右侧时,根据题意画出图形
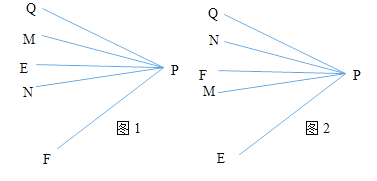
如图1:∵射线PM平分![]() ,射线
,射线![]() 平分
平分![]() .
.
∴![]() ,
,![]()
∴![]()
∵![]() 和
和![]() 互余,
互余,![]()
∴![]()
∴![]()
如图2∵PM平分![]() ,射线
,射线![]() 平分
平分![]() .
.
∴![]() ,
,![]()
∴![]()
∵![]() 和
和![]() 互余,
互余,![]()
∴![]()
∴![]()
综上所述可得:![]() =45°或
=45°或![]()
故答案为:45°或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,假命题有( )
①两点之间线段最短;
②到角的两边距离相等的点在角的平分线上;③过一点有且只有一条直线与已知直线平行;
④垂直于同一直线的两条直线平行;⑤若
 的弦AB,CD交于点P,则
的弦AB,CD交于点P,则
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知图甲是一个长为2m、宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.

(1)图乙中阴影部分正方形的边长为________(用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一:________________;
方法二:________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.
下列四种说法:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.
其中,正确的有( ) 个.

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAB中,OA=OB=10cm,∠AOB=80°,以点O为圆心,半径为6cm的优弧弧MN分别交OA,OB于点M,N.
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;
(2)点T在左半弧上,若AT与弧相切,求AT的长.

相关试题

