【题目】下列命题中,假命题有( )
①两点之间线段最短;
②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;
④垂直于同一直线的两条直线平行;
⑤若![]() 的弦AB,CD交于点P,则
的弦AB,CD交于点P,则![]()
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】分析: 根据线段的性质公理判断①;
根据角平分线的性质判断②;
根据垂线的性质、平行公理的推论判断③④;
连接AC、DB,根据同弧所对的圆周角相等,证出△ACP∽△DBP,然后根据相似三角形的性质得出结论.依此判断⑤.
详解: ①两点之间线段最短,说法正确,不是假命题;
②到角的两边距离相等的点在角的平分线上,说法正确,不是假命题;
③过直线外一点有且只有一条直线与已知直线平行,原来的说法错误,是假命题;
④在同一平面内,垂直于同一直线的两条直线平行,原来的说法错误,是假命题;
⑤ 如图,连接AC、BD.
如图,连接AC、BD.
∵∠A=∠D,∠C=∠B,
∴△ACP∽△DBP,
∴PAPD=PCPB,
∴PAPB=PCPD,
故若⊙O的弦AB,CD交于点P,则PAPB=PCPD的说法正确,不是假命题。
故选:C.
点睛: 本题考查了线段的性质公理,角平分线的性质,垂线的性质,平行公理的推论,点相交弦定理,是基础知识,需熟练掌握.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,四个不同的点
 分别表示有理数
分别表示有理数 ,且
,且 .
.(1)如图1,
 为线段
为线段 的中点,
的中点,
①当点
 与原点
与原点 重合时,用等式表示
重合时,用等式表示 与
与 的关系为 ;
的关系为 ;②求点
 表示的有理数
表示的有理数 的值(用含
的值(用含 的代数式表示);
的代数式表示);(2)已知
 ,
,①若三点
 的位置如图所示,请在图中标出点
的位置如图所示,请在图中标出点 的位置;
的位置;
②
 的大小关系为 (用“
的大小关系为 (用“ ”连接)
”连接) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)12-(-18)+(-5)-6;
(2)12÷(-
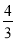 )×8;
)×8;(3)2-2÷(-
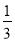 )×3;
)×3; (4)-12+
 ×(-2)3+ (-3)2;
×(-2)3+ (-3)2;(5)(-
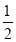 -
-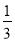 +
+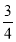 )×(-60).
)×(-60). -
科目: 来源: 题型:
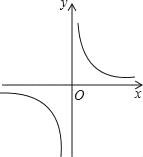
查看答案和解析>>【题目】反比例函数
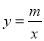 的图象如图所示,以下结论:
的图象如图所示,以下结论:①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知图甲是一个长为2m、宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.

(1)图乙中阴影部分正方形的边长为________(用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一:________________;
方法二:________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.
下列四种说法:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.
其中,正确的有( ) 个.

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:小聪遇到这样一个问题: 如图1,
 ,请画一个
,请画一个 ,使
,使 与
与 互补.
互补.
小聪是这样思考的:首先通过分析明确射线
 在
在 的外部,画出示意图,如图2所示:然后通过构造平角找到
的外部,画出示意图,如图2所示:然后通过构造平角找到 的补角
的补角 ,
,
如图3所示:进而分析要使
 与
与 互补,则需
互补,则需 .
.
因此,小聪找到了解决问题的方法:反向延长射线
 得到射线
得到射线 ,利用量角器画出
,利用量角器画出 的平分线
的平分线 ,这样就得到了
,这样就得到了 与
与 互补
互补(1)小聪根据自己的画法写出了己知和求证,请你完成证明.已知:如图3,点
 在直线
在直线 上,射线
上,射线 平分
平分 .求证:
.求证:  与
与 互补. .
互补. .
(2)参考小聪的画法,请在下图中画出--个
 ,使
,使 与
与 互余.(保留画图痕迹)
互余.(保留画图痕迹)
(3)已知
 和
和 互余,射线
互余,射线 平分
平分 ,射线
,射线 平分
平分 .若
.若 ,直接写出锐角
,直接写出锐角 的度数是 .
的度数是 .
相关试题

