【题目】(方案设计题)如图是人民公园中的荷花池,现要测量荷花池岸边树A与树B间的距离.如果直接测量比较困难,请你根据所学知识,以卷尺和测角仪为测量工具,设计两种不同的测量方案并画出图形.

参考答案:
【答案】见解析
【解析】
根据全等三角形的判定,构造全等三角形,利用全等三角形的性质可推出AB的距离.
解:方案一:如图甲,(1)在平地上取一个可以直接到达A点和B点的点O,连接AO并延长到C,使OC=OA;(2)连接BO并延长到D,使OD=OB;(3)连接CD,则线段CD的长度即为树A与树B之间的距离.
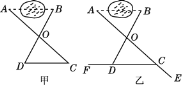
方案二:如图乙,(1)在直线AB外取一点E,用测角仪测得∠BAE=α;
(2)在射线AE上取两点O和C,使OA=OC;
(3)在射线AE一侧取一点F,使∠ACF=α;
(4)连接BO并延长交射线CF于点D,则线段CD的长度即为树A与树B之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。

(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,y随x的增大而增大的是( )
A.y=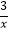
B.y=﹣x+5
C.y= x
x
D.y=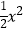 (x<0)
(x<0) -
科目: 来源: 题型:
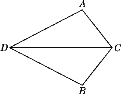
查看答案和解析>>【题目】如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线,一轮船离开码头,计划沿∠ADB的平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.
-
科目: 来源: 题型:
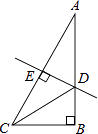
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( )
A.2
B.2
C.4
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c的图象如图所示,顶点为(4,6),则下列说法错误的是( )

A.b2>4ac
B.ax2+bx+c≤6
C.若点(2,m)(5,n)在抛物线上,则m>n
D.8a+b=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,从顶点A引两条射线分别交BC,CD于点E,F,且∠EAF=45°.
求证:BE+DF=EF.

相关试题

