Question

【题目】已知：二次函数的图象与x轴交于A、B两点(点A在点B的左侧)，与y轴交于点C，对称轴是直线x=1，且图象向右平移一个单位后经过坐标原点O,

(1)求这个二次函数的解析式；

(2)直线交y轴于D点，E为抛物线顶点.若∠DBC=α，∠CBE=β，求α-β的值.

(3)在(2)问的前提下，P为抛物线对称轴上一点，且满足PA=PC，在y轴右侧的抛物线上是否存在点M，使得△BDM的面积等于PA2若存在，求出点M的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）这个二次函数的解析式为；

（2）α-β=45°

（3）综上所述，存在符合条件的点M其坐标为或.

【解析】分析： (1)根据二次函数的对称性可求得点B的坐标，将它们代入抛物线的解析式中，通过联立方程组求得待定系数的值，即可确定该抛物线的解析式；

(2)根据抛物线和直线BD的解析式，可求得C、D、E的坐标，即可得到∠OBC=∠OCB=45 °；所求角的度数差可转化为∠OBC的度数；在Rt△OBC中，已经求得∠OBC=∠OCB=45 °，由此得解；

(3)易知抛物线的对称轴方程，可设出点P的解析式，求出点P的坐标，进而得到PA的值，即可求得△BDM的面积．可用面积割补法求解.

本题解析：

(1)由题意，A(-1,0)

对称轴是直线x=1

∴B(3,0)

把A(-1,0)，B(3,0)分别代入y=ax-2x+c得

解得

∴这个二次函数的解析式为y=x-2x-3

(2) ∵直线 与y轴交于D(0,1), ∴OD=1

由Y=X-2X-3=(x-1)-4得E91，-4）

连接CE过E作EF⊥y轴于F(如图1)，则EF=1

∵抛物线y=x-2x-3与y轴交于C90，-3

∴OC=OB=3，CF=1=EF

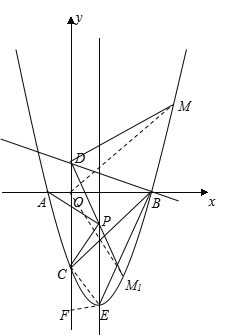
(如图1)

∴∠OBC=∠OCB=∠FCE=45°,

BC=,CE=

∴∠BCE=90°=∠BOD, ,

∴

∴△BOD∽△BCE

∴∠CBF=∠DBO

∴

(3)设P(1，n)

∵PA=PC

∴PA=PC, 即(1+1)+(n-0)=(1+0)+(n+3)

解得n=-1

∴PA=(1+1)+(-1-0)=5

∴

方法一：设存在符合条件的点M(m,m-2m-3),则m>0

①当M在直线BD上侧时，连接OM(如图1)，

则

即

整理，得

解得 (舍去)，

把代入 得

∴

②当M在直线BD下侧时，不妨叫连接 (如图1)，

则

即

整理，得

解得 (舍去)

把m=2代入 得y=-3

∴

综上所述，存在符合条件的点M其坐标为或(2,-3).

方法二：设存在符合条件的点，则m>0

①当M在直线BD上侧时，过M作MG∥y轴，交DB于G(如图2)

设D、B到MG距离分别为则

即 , ,

整理，得

解得 (舍去)，

把代入y=m-2m-3得y=

∴M()

②当M在直线BD下侧时，不妨叫过作∥y轴，交DB于 (如图2)

设D、B到距离分别为则

即

整理，得3m-5m-2=0

解得 (舍去)

把m=2代入y=m-2m-3得y=-3

∴

综上所述，存在符合条件的点M其坐标为或(2,-3)

方法三：①当M在直线BD上侧时，过M作MH∥BD交y轴于H,连接BH(如图3)

则,即

∴DH=

∴H(0, )

∴直线BH解析式为y=

联立 得 或

M在y轴右侧, ∴M坐标为

②当M在直线BD下侧时，不妨叫 过作∥BD，交y轴于,

连接B (如图3)，同理可得D=

∴ (0, )

∴直线 解析式为

联立得或

∵在y轴右侧，∴坐标为(2,-3)

综上所述，存在符合条件的点M,其坐标为或(2,-3).