【题目】已知二次函数y=(t+1)x2+2(t+2)x+ ![]() 在x=0和x=2时的函数值相等.
在x=0和x=2时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数y=kx+6的图象与二次函数的图象都经过点A(﹣3,m),求m和k的值;
(3)把二次函数的图象与x轴两个交点之间的部分记为图象G,把图象G向左平移n(n>0)个单位后得到的图象记为M,请结合图象回答:当(2)中得到的直线与图象M有公共点时,求n的取值范围.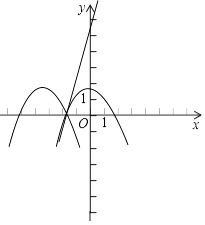
参考答案:
【答案】
(1)解:∵二次函数y=(t+1)x2+2(t+2)x+ ![]() 在x=0和x=2时的函数值相等,
在x=0和x=2时的函数值相等,
∴对称轴x=﹣ ![]() =
= ![]() =1,解得,t=﹣
=1,解得,t=﹣ ![]() ,
,
则二次函数的解析式为:y=(﹣ ![]() +1)x2+2(﹣
+1)x2+2(﹣ ![]() +2)x+
+2)x+ ![]() ,即y=﹣
,即y=﹣ ![]() (x+1)(x﹣3)或y=﹣
(x+1)(x﹣3)或y=﹣ ![]() (x﹣1)2+2,
(x﹣1)2+2,
(2)解:∵二次函数的象经过点A(﹣3,m),
∴m=﹣ ![]() (﹣3+1)(﹣3﹣3)=﹣6.
(﹣3+1)(﹣3﹣3)=﹣6.
又∵一次函数y=kx+6的图象经过点A(﹣3,m),;
∴m=﹣3k+6,即﹣6=﹣3k+6,
解得,k=4.
综上所述,m和k的值分别是﹣6、4;
(3)解:由题意可知,图象G的解析式是y=﹣ ![]() x2+x+
x2+x+ ![]() =﹣
=﹣ ![]() (x2﹣2x﹣3)=﹣
(x2﹣2x﹣3)=﹣ ![]() (x﹣3)(x+1),﹣1≤x≤3,
(x﹣3)(x+1),﹣1≤x≤3,
则抛物线平移后得出的图象M的解析式是y=﹣ ![]() (x﹣3+n)(x+1+n),﹣n﹣1≤x≤3﹣n,
(x﹣3+n)(x+1+n),﹣n﹣1≤x≤3﹣n,
此时直线平的解析式是y=4x+6,
如果直线与平移后的二次函数相切,
则方程4x+6=﹣ ![]() (x﹣3+n)(x+1+n)有两个相等的实数解,
(x﹣3+n)(x+1+n)有两个相等的实数解,
即x2+(2n+6)x+n2﹣6n+9=0有两个相等的实数解,。
判别式△=(2n+6)2﹣4×(n2﹣6n+9)=48n=0,
即n=0,
∵与已知n>0相矛盾,
∴平移后的直线与平移后的抛物线不相切,
∴结合图象可知,如果平移后的直线与抛物线有公共点,
则两个临界的交点为(﹣n﹣1,0),(3﹣n,0),
则0=4(﹣n﹣1)+6,
n= ![]() ,
,
0=4(3﹣n)+6,
n= ![]() ,
,
即n的取值范围是: ![]() ≤n≤
≤n≤ ![]() .
.
【解析】(1)根据已知条件知,该函数的对称轴方程为x=1,从而根据对称轴公式建立出关于t的方程,求出t的值,把t的值代入函数解析式即可,根据图像与坐标轴的交点坐标,顶点坐标画出图像;
(2)求出A点的坐标,再用待定系数法求出k的值;
(3)由题意可知,图象G的解析式是y=﹣ ![]() (x﹣3)(x+1),(﹣1≤x≤3,)得出抛物线平移后得出的图象M的解析式是y=﹣
(x﹣3)(x+1),(﹣1≤x≤3,)得出抛物线平移后得出的图象M的解析式是y=﹣ ![]() (x﹣3+n)(x+1+n),(﹣n﹣1≤x≤3﹣n),此时直线平的解析式是y=4x+6,如两图像有一个交点时,得出方程方程4x+6=﹣
(x﹣3+n)(x+1+n),(﹣n﹣1≤x≤3﹣n),此时直线平的解析式是y=4x+6,如两图像有一个交点时,得出方程方程4x+6=﹣ ![]() (x﹣3+n)(x+1+n)有两个相等的实数解,求出判别式△=(2n+6)2﹣4×(n2﹣6n+9)=48n=0,求出n的值与已知的值矛盾,得出平移后的直线与抛物线有两个公共点,设出两个临界的交点为(﹣n﹣1,0),(3﹣n,0),代入直线的解析式求出n的值,即可得出答案
(x﹣3+n)(x+1+n)有两个相等的实数解,求出判别式△=(2n+6)2﹣4×(n2﹣6n+9)=48n=0,求出n的值与已知的值矛盾,得出平移后的直线与抛物线有两个公共点,设出两个临界的交点为(﹣n﹣1,0),(3﹣n,0),代入直线的解析式求出n的值,即可得出答案
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
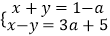 (a≥0),给出下列说法:
(a≥0),给出下列说法:
①当a=1时,方程组的解也是方程x+y=2的一个解;
②当x﹣2y>8时,a>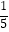 ;
;
③不论a取什么实数,2x+y的值始终不变;
④某直角三角形的两条直角边长分别为x+y,x﹣y,则其面积最大值为 .
.
以上说法正确的是( )
A.②③
B.①②④
C.③④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型
甲
乙
丙
汽车运载量(吨/辆)


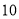
汽车运费(元/辆)



(1)若全部物资都用甲、乙两种车型来运送,需运费
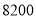 元,问分别需甲、乙两种车型各几辆?
元,问分别需甲、乙两种车型各几辆?(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知他们的总辆数为
 辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
辆,你能通过列方程组的方法分别求出几种车型的辆数吗?(3)求出哪种方案的运费最省?最省是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,O为线段AB上一点,AB=6,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.

(1)若AO=4,
①当t=1秒时,OP= , S△ABP=;
②当△ABP是直角三角形时,求t的值;
(2)如图2,若点O为AB中点,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求AQBP的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①
 ,又
,又 ,
, ,∴能确定59319的立方根是个两位数.
,∴能确定59319的立方根是个两位数.②∵59319的个位数是9,又
 ,∴能确定59319的立方根的个位数是9.
,∴能确定59319的立方根的个位数是9.③如果划去59319后面的三位319得到数59,
而
 ,则
,则 ,可得
,可得 ,
,由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数195112,按这种方法求立方根,请完成下列填空.
①它的立方根是_______位数.
②它的立方根的个位数是_______.
③它的立方根的十位数是__________.
④195112的立方根是________.
(2)请直接填写结果:
①
 ________.
________.②
 ________.
________. -
科目: 来源: 题型:
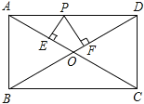
查看答案和解析>>【题目】如图,矩形ABCD的两边AB=3,BC=4,P是AD上任一点,PE⊥AC于点E,PF⊥BD于点F.求PE+PF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B、D为线段AH上两点,△ABC、△BDE和△DGH都是等边三角形,连结CE并延长交AH的延长线于点F,点G恰好在CF上,△ABC的外接圆⊙O交CF于点M.
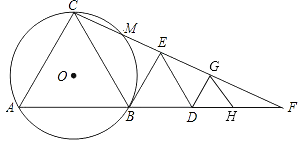
(1)求证:AC 2=CMCF;
(2)若CM=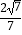 ,MF=
,MF= 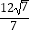 ,求圆O的半径长;
,求圆O的半径长;
(3)设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3 , 请直接写出S1、S2、S3之间的等量关系.
相关试题

