搜索
【题目】已知关于x、y的方程组 
（a≥0），给出下列说法：
①当a=1时，方程组的解也是方程x+y=2的一个解；
②当x﹣2y＞8时，a＞ 
；
③不论a取什么实数，2x+y的值始终不变；
④某直角三角形的两条直角边长分别为x+y，x﹣y，则其面积最大值为 
．
以上说法正确的是（ ）
A.②③
B.①②④
C.③④
D.②③④
参考答案：
【答案】C
【解析】解：已知关于x、y的方程组 
（a≥0），解得： 
，给出下列说法：①当a=1时，方程组的解也是方程x+y=0的一个解，不符合题意；②当x﹣2y=a+3+4a+8＞8时，a＞﹣ 
，不符合题意；③不论a取什么实数，2x+y=2的值始终不变，符合题意；④某直角三角形的两条直角边长分别为x+y=﹣a﹣1，x﹣y=3a+7，则其面积最大值为 
，符合题意．
所以答案是：C
【考点精析】本题主要考查了二元一次方程的解和二元一次方程组的解的相关知识点，需要掌握适合一个二元一次方程的一组未知数的值，叫做这个二元一次方程的一个解；二元一次方程组中各个方程的公共解，叫做这个二元一次方程的解才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将下列方格纸中的△ABC向右平移7格，再向下平移2格，得到△
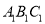．（1）画出平移后的三角形； （2）若AB=5，则
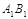= ． （3）连接AA1,BB1, 根据“图形平移”的性质,得：线段AA1与线段BB1的数量关系和位置关系是: ．
（4）求图中∠
AC+∠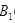
BC的度数．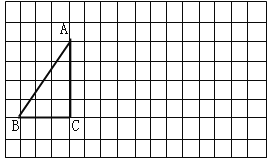 
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校260名学生参加植树活动，要求每人植4﹣7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵，将这四类的人数绘制成扇形图（如图1）和条形图（如图2）．
经确认扇形图是正确的，而条形图尚有一处错误．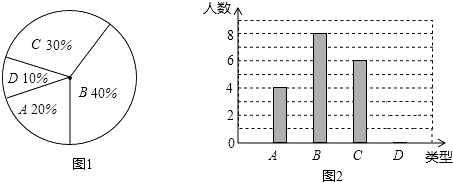
回答下列问题：
（1）写出条形图中存在的错误为；
（2）写出这20名学生每人植树量的众数为；中位数为；
（3）经计算这20名学生每人植树量的平均数为5.3，则估算这260名学生共植树棵．
（4）在这次活动中，九（1）班学生平均每人植6棵树，如果单独由男同学完成，每人应植树15棵，求如果单独由女同学完成，每人应植树多少棵？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB是⊙O的弦，半径OA=2cm，∠AOB=120°
（1）求tan∠OAB的值；
（2）求图中阴影部分的面积S；
（3）在⊙O上一点P从A点出发，沿逆时针方向运动一周，回到点A，在点P的运动过程中，满足S△POA=S△AOB时，直接写出P点所经过的弧长（不考虑点P与点B重合的情形）． -
科目： 来源： 题型：
查看答案和解析>>【题目】一方有难八方支援，某市政府筹集了抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
车型
甲
乙
丙
汽车运载量（吨/辆）
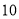
汽车运费（元/辆）
（1）若全部物资都用甲、乙两种车型来运送，需运费
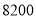元，问分别需甲、乙两种车型各几辆？（2）为了节约运费，该市政府可以调用甲、乙、丙三种车型参与运送，已知他们的总辆数为
辆，你能通过列方程组的方法分别求出几种车型的辆数吗？（3）求出哪种方案的运费最省？最省是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，O为线段AB上一点，AB=6，OC为射线，且∠BOC=60°，动点P以每秒2个单位长度的速度从点O出发，沿射线OC做匀速运动，设运动时间为t秒．
（1）若AO=4，
①当t=1秒时，OP= ， S△ABP=；
②当△ABP是直角三角形时，求t的值；
（2）如图2，若点O为AB中点，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求AQBP的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=（t+1）x2+2（t+2）x+
在x=0和x=2时的函数值相等．
（1）求二次函数的解析式；
（2）若一次函数y=kx+6的图象与二次函数的图象都经过点A（﹣3，m），求m和k的值；
（3）把二次函数的图象与x轴两个交点之间的部分记为图象G，把图象G向左平移n（n＞0）个单位后得到的图象记为M，请结合图象回答：当（2）中得到的直线与图象M有公共点时，求n的取值范围．
相关试题
