【题目】如图,B、D为线段AH上两点,△ABC、△BDE和△DGH都是等边三角形,连结CE并延长交AH的延长线于点F,点G恰好在CF上,△ABC的外接圆⊙O交CF于点M.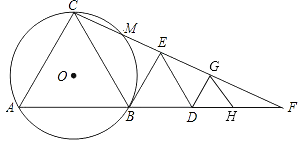
(1)求证:AC 2=CMCF;
(2)若CM= ![]() ,MF=
,MF= ![]() ,求圆O的半径长;
,求圆O的半径长;
(3)设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3 , 请直接写出S1、S2、S3之间的等量关系.
参考答案:
【答案】
(1)解:连结MB,则∠CMB=180°﹣∠A=120°,
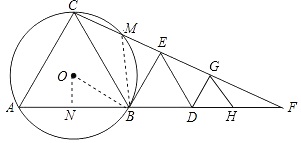
∵∠CBF=60°+60°=120°,
∴∠CMB=∠CBF,
∵∠BCM=∠FCB,
∴△CMB∽△CBF,
∴ ![]() ,即CB2=CMCF,
,即CB2=CMCF,
∵AC=CB,
∴AC2=CMCF
(2)解:过点O作ON⊥AB于点N,
则∠CMB=120°,
∵∠CBF=120°,
∴∠CMB=∠CBF,
∵∠BCF=∠BCM,
∴△CMB∽△CBF,
∴ ![]() =
= ![]() ,
,
即CB2=CMCF,
∵AC=CB=AB,CM= ![]() ,MF=
,MF= ![]() ,
,
∴CB2= ![]() ,
,
AB=AC=BC= ![]() ,
,
∵△ABC是等边三角形,
∴∠OBA=30°,
∴ON= ![]() BO,
BO,
∴cos30°= ![]() =
= ![]() =
= ![]() ,
,
解得:BO= ![]() ,
,
即⊙O的半径为: ![]() ;
;
(3)解:由题意可得:AC∥BE∥DG,BC∥DE∥HG,
∴ ![]() =
= ![]() =
= ![]()
∵ ![]() =(
=( ![]() )2
)2
![]() =(
=( ![]() )2
)2
∴ ![]() =
= ![]() 即S22=S1S3
即S22=S1S3
∴所求的数量关系是S22=S1S3.
【解析】1)连结MB易证∠CMB=∠CBF,则可以得到△CMB∽△CBF,根据相似三角形对应边的比相等即可证明;
(2)过点O作ON⊥AB于点N,易证∠CMB=∠CBF,则可以得到△CMB∽△CBF,根据相似三角形对应边的比相等即可得AB=AC=BC,从而得出△ABC是等边三角形,故∠OBA=30°,根据含30![]() 直角三角形的边之间的关系得出ON=
直角三角形的边之间的关系得出ON= ![]() BO,根据特殊锐角的三角函数值及锐角三角函数的定义列出方程求解即可;
BO,根据特殊锐角的三角函数值及锐角三角函数的定义列出方程求解即可;
(3)由题意可得:AC∥BE∥DG,BC∥DE∥HG,根据平行线分线段成比例定理及相似三角形的性质即可得出结论。
【考点精析】认真审题,首先需要了解平行线分线段成比例(三条平行线截两条直线,所得的对应线段成比例),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=(t+1)x2+2(t+2)x+
 在x=0和x=2时的函数值相等.
在x=0和x=2时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数y=kx+6的图象与二次函数的图象都经过点A(﹣3,m),求m和k的值;
(3)把二次函数的图象与x轴两个交点之间的部分记为图象G,把图象G向左平移n(n>0)个单位后得到的图象记为M,请结合图象回答:当(2)中得到的直线与图象M有公共点时,求n的取值范围.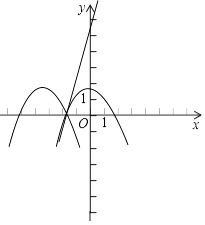
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①
 ,又
,又 ,
, ,∴能确定59319的立方根是个两位数.
,∴能确定59319的立方根是个两位数.②∵59319的个位数是9,又
 ,∴能确定59319的立方根的个位数是9.
,∴能确定59319的立方根的个位数是9.③如果划去59319后面的三位319得到数59,
而
 ,则
,则 ,可得
,可得 ,
,由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数195112,按这种方法求立方根,请完成下列填空.
①它的立方根是_______位数.
②它的立方根的个位数是_______.
③它的立方根的十位数是__________.
④195112的立方根是________.
(2)请直接填写结果:
①
 ________.
________.②
 ________.
________. -
科目: 来源: 题型:
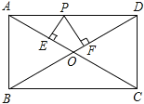
查看答案和解析>>【题目】如图,矩形ABCD的两边AB=3,BC=4,P是AD上任一点,PE⊥AC于点E,PF⊥BD于点F.求PE+PF的值.
-
科目: 来源: 题型:
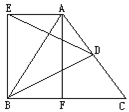
查看答案和解析>>【题目】已知,如图,等边△ABC中,AD=DC,BF=FC,△BDE是等边三角形.求证:四边形AEBF是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
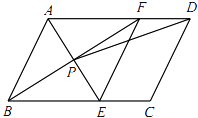
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①平面内,垂直于同一直线的两条直线平行;②两条直线被第三条直线所截,内错角相等;③如果直线
 ,
, 那么
那么 ;④直线外一点与直线上各点连接的所有线段中,垂线段最短;⑤同旁内角的角平分线互相垂直.其中正确的是( )
;④直线外一点与直线上各点连接的所有线段中,垂线段最短;⑤同旁内角的角平分线互相垂直.其中正确的是( )A.①③④B.①②⑤C.②③④D.②③⑤
相关试题

