搜索
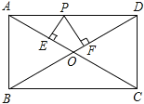
【题目】如图，矩形ABCD的两边AB=3，BC=4，P是AD上任一点，PE⊥AC于点E，PF⊥BD于点F.求PE+PF的值.
参考答案：
【答案】
【解析】
首先连接OP．由矩形ABCD的两边AB=3，BC=4，可求得OA=OD=
，S△AOD=
S矩形ABCD然后由S△AOD=S△AOP+S△DOP=
OAPE+ODPF=OA（PE+PF）=
×（PE+PF）=3，求得答案．
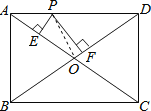
解：连接OP，
∵矩形ABCD的两边AB=3，BC=4，
∴S矩形ABCD=ABBC=12，OA=OC，OB=OD，AC=BD，AC=
=5，
∴S△AOD=S矩形ABCD=3，OA=OD=，
∵PE⊥AC， PF⊥BD
∴S△AOD=S△AOP+S△DOP=OAPE+ODPF=OA（PE+PF）=×（PE+PF）=3，
∴PE+PF=．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，O为线段AB上一点，AB=6，OC为射线，且∠BOC=60°，动点P以每秒2个单位长度的速度从点O出发，沿射线OC做匀速运动，设运动时间为t秒．
（1）若AO=4，
①当t=1秒时，OP= ， S△ABP=；
②当△ABP是直角三角形时，求t的值；
（2）如图2，若点O为AB中点，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求AQBP的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=（t+1）x2+2（t+2）x+
在x=0和x=2时的函数值相等．
（1）求二次函数的解析式；
（2）若一次函数y=kx+6的图象与二次函数的图象都经过点A（﹣3，m），求m和k的值；
（3）把二次函数的图象与x轴两个交点之间的部分记为图象G，把图象G向左平移n（n＞0）个单位后得到的图象记为M，请结合图象回答：当（2）中得到的直线与图象M有公共点时，求n的取值范围．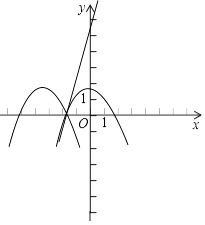
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根．华罗庚脱口而出：39．众人感觉十分惊奇，请华罗庚给大家解读其中的奥秘．
你知道怎样迅速准确的计算出结果吗？请你按下面的问题试一试：
①
，又
，
，∴能确定59319的立方根是个两位数．②∵59319的个位数是9，又
，∴能确定59319的立方根的个位数是9．③如果划去59319后面的三位319得到数59，
而
，则
，可得
，由此能确定59319的立方根的十位数是3
因此59319的立方根是39．
（1）现在换一个数195112，按这种方法求立方根，请完成下列填空．
①它的立方根是_______位数．
②它的立方根的个位数是_______．
③它的立方根的十位数是__________．
④195112的立方根是________．
（2）请直接填写结果：
①
________．②
________． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，B、D为线段AH上两点，△ABC、△BDE和△DGH都是等边三角形，连结CE并延长交AH的延长线于点F，点G恰好在CF上，△ABC的外接圆⊙O交CF于点M．
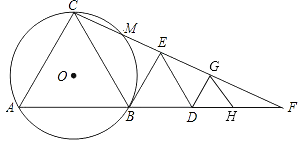
（1）求证：AC 2=CMCF；
（2）若CM=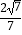
，MF=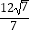 
，求圆O的半径长；
（3）设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3 ， 请直接写出S1、S2、S3之间的等量关系． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，等边△ABC中，AD=DC，BF=FC，△BDE是等边三角形．求证：四边形AEBF是矩形．
-
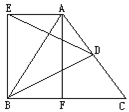
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，AE平分∠BAD，交BC于点E，BF平分∠ABC，交AD于点F，AE与BF交于点P，连接EF，PD．
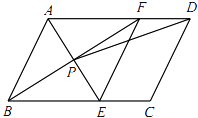
（1）求证：四边形ABEF是菱形；
（2）若AB=4，AD=6，∠ABC=60°，求tan∠ADP的值．
相关试题
