搜索
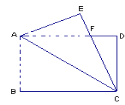
【题目】如图，在长方形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F.
（1）试说明：AF=FC；（2）如果AB=12，BC=16，求AF的长
参考答案：
【答案】（1）证明见解析；（2）12.5.
【解析】
（1）根据折叠的性质可得∠ACB=∠ACF，根据矩形的性质可得∠ACB=∠CAF，则即可得证；
（2）设AF=x，则DF=16﹣x，在Rt△CDF中，利用勾股定理得到关于x的方程，然后求解方程即可.
解：（1）∵四边形ABCD为矩形，△ABC与△AEC关于AC对称，
∴∠ACB=∠CAF，∠ACB=∠ACF，
∴∠CAF=∠ACF，
∴AF=FC；
（2）设AF=x，则DF=16﹣x，
在Rt△CDF中，CF2=DF2+CD2，
∴x2=（16﹣x）2+122，
解得x=12.5.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在四边形ABCD中，∠B＝∠D＝90°，AB＝BC＝15千米，CD＝3
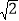千米．求四边形ABCD的周长和面积(结果保留整数，参考数据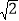：≈1.41，
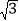≈1.73，
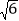≈2.45)．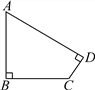
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示,在边长为a米的正方形草坪上修建两条宽为b米的道路.
（1）为了求得剩余草坪的面积，小明同学想出了两种办法，结果分别如下：
方法①： 方法②：
请你从小明的两种求面积的方法中，直接写出含有字母a，b代数式的等式是：
（2）根据（1）中的等式，解决如下问题：
①已知：
，求
的值；②己知：
，求
的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，两幢建筑物AB和CD，AB⊥BD，CD⊥BD，AB＝15m，CD＝20m，AB和CD之间有一观景池，小南在A点测得池中喷泉处E点的俯角为42°，在C点测得E点的俯角为45°(点B、E、D在同一直线上)，求两幢建筑物之间的距离BD.(结果精确到0.1m).
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在长方形ABCD中，AB=8cm，BC=12cm，点E为AB中点，如果点P在线段BC上以每秒4cm的速度，由点B向点C运动，同时，点Q在线段CD上以v厘米/秒的速度，由点C向点D运动，设运动时间为t秒.
（1）直接写出：PC= 厘米，CQ= 厘米；(用含t、v的代数式表示)
（2）若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等，试求v、t的值；
（3）若点Q以（2）中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针方向沿长方形ABCD的四边运动，求经过多长时间点P与点Q第一次在长方形ABCD的哪条边上相遇？
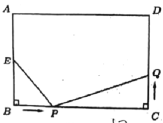
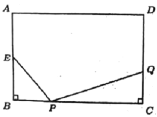
备用图
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，
，
.求
的度数.
请将求
的度数的过程及理由填写出来.解：∵
（已知），∴
（______________________）.又∵
（已知），∴
（______________________）.∴
__________（______________________）.∴
__________
（______________________）.又∵
（已知），∴
_________. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP.
（1）求证：直线CP是⊙O的切线；
（2）若BC=2
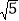，sin∠BCP=
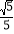，求⊙O的半径及△ACP的周长.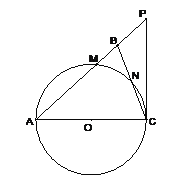
相关试题
