【题目】如图所示,在边长为a米的正方形草坪上修建两条宽为b米的道路.
(1)为了求得剩余草坪的面积,小明同学想出了两种办法,结果分别如下:
方法①: 方法②:
请你从小明的两种求面积的方法中,直接写出含有字母a,b代数式的等式是:
(2)根据(1)中的等式,解决如下问题:
①已知:![]() ,求
,求![]() 的值;
的值;
②己知:![]() ,求
,求![]() 的值.
的值.

参考答案:
【答案】(1)(a-b)2;a2-2ab+b2;(a-b)2=a2-2ab+b2;(2)ab=-2.5;(x-2019)2=5.
【解析】
(1)方法①是根据已知条件先表示出矩形的长和宽,再根据矩形的面积公式即可得出答案;方法②是正方形的面积减去两条道路的面积,即可得出剩余草坪的面积;根据(1)得出的结论可得出![]() ;
;
(2)①分别把![]() 的值和
的值和![]() 的值代入(1)中等式,即可得到答案;
的值代入(1)中等式,即可得到答案;
②根据题意,把(x-2018)和(x-2020)变成(x-2019)的形式,然后计算完全平方公式,展开后即可得到答案.
解:(1)方法①:草坪的面积=(a-b)(a-b)=![]() .
.
方法②:草坪的面积=![]() ;
;
等式为:![]()
故答案为:![]() ,
,![]() ;
;![]()
(2)①把![]() 代入
代入![]()
∴![]() ,
,
∴![]()
②原式可化为:![]()
∴![]()
∴![]()
∴![]()
-
科目: 来源: 题型:
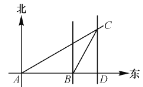
查看答案和解析>>【题目】如图,已知某船于上午8点在A处观测小岛C在北偏东60°方向上.该船以每小时30海里的速度向东航行到B处,此时测得小岛C在北偏东30°方向上.船以原速度再继续向东航行1.5小时到达小岛C的正南方D点.求船从A到D一共走了多少海里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且BF=CE
求证:(1)△ABC是等腰三角形
(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,证明你的结论

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形ABCD中,∠B=∠D=90°,AB=BC=15千米,CD=3
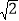 千米.求四边形ABCD的周长和面积(结果保留整数,参考数据:
千米.求四边形ABCD的周长和面积(结果保留整数,参考数据: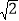 ≈1.41,
≈1.41,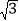 ≈1.73,
≈1.73,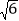 ≈2.45).
≈2.45).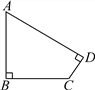
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m,AB和CD之间有一观景池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD.(结果精确到0.1m).

-
科目: 来源: 题型:
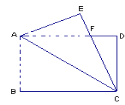
查看答案和解析>>【题目】如图,在长方形ABCD中,将△ABC沿AC对折至△AEC位置,CE与AD交于点F.
(1)试说明:AF=FC;(2)如果AB=12,BC=16,求AF的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=8cm,BC=12cm,点E为AB中点,如果点P在线段BC上以每秒4cm的速度,由点B向点C运动,同时,点Q在线段CD上以v厘米/秒的速度,由点C向点D运动,设运动时间为t秒.
(1)直接写出:PC= 厘米,CQ= 厘米;(用含t、v的代数式表示)
(2)若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等,试求v、t的值;
(3)若点Q以(2)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针方向沿长方形ABCD的四边运动,求经过多长时间点P与点Q第一次在长方形ABCD的哪条边上相遇?
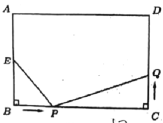
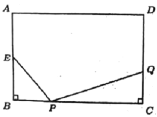
备用图
相关试题

