【题目】(1)在数轴上表示下列各数,并用“<”号把它们连接.
3, -1, 0, -2.5, 1.5, 2![]()
(2)快递员要从物流中心出发送货,已知甲住户在物流中心的东边 2km 处,乙住户在甲住户的西边 3km 处,丙住户在物流中心的西边 1.5km 处,请建立数轴表示物流中心、甲住户、乙住户、丙住户的位置关系.
参考答案:
【答案】(1)图详见解析(2)图详见解析
【解析】
(1)画出数轴,注意数轴的三要素,原点,正方向,单位长度要体现出来,然后把以上各数在原点上以点的形式表示出来,最后按照左边的数小于右边的数进行排列.
(2)以物流中心为原点,正方向为东方,单位长度为1km,建立数轴,表示出各个位置.
(1)

由数轴可知,左边的数小于右边的数,则![]()
(2)以物流中心为原点,正方向为东,单位长度为1km,则甲所在位置为+2km,乙所在位置为+2-3=-1km,丙所在位置为0-1.5=-1.5km.如图所示:

-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 80° B. 90° C. 100° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上点
 表示数
表示数 ,点
,点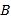 表示数
表示数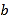 ,点
,点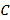 表示数
表示数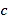 ,
,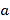 是多项式
是多项式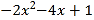 的一次项系数,
的一次项系数,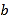 是绝对值最小的整数,单项式
是绝对值最小的整数,单项式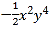 的次数为
的次数为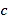 .
.
(1)
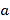 = ,
= ,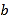 = ,
= , = ;
= ;(2)若将数轴在点
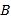 处折叠,则点
处折叠,则点 与点
与点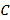 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);(3)点
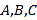 开始在数轴上运动,若点
开始在数轴上运动,若点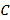 以每秒1个单位长度的速度向右运动,同时,点
以每秒1个单位长度的速度向右运动,同时,点 和点
和点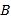 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,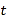 秒钟过后,若点
秒钟过后,若点 与点B之间的距离表示为
与点B之间的距离表示为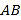 ,点
,点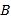 与点
与点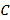 之间的距离表示为
之间的距离表示为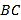 ,则
,则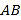 = ,
= ,  = (用含
= (用含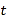 的代数式表示);
的代数式表示);(4)请问:AB+BC的值是否随着时间
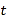 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一刻度尺放在数轴上.

①若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为 1 和 5,则 1cm 对应数轴上的点表示的数是 2;
②若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为 1 和 9,则 1cm 对应数轴上的点表示的数是 3;
③若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为-2 和 2,则 1cm 对应数轴上的点表示的数是-1;
④若刻度尺上 0cm 和 4 cm 对应数轴上的点表示的数分别为-1 和 1,则 1cm 对应数轴上的点表示的数是-0.5. 上述结论中,所有正确结论的序号是 ( )
A.①②B.②④C.①②③D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…,依次规律,第( )个图形有76个小圆.

A. 8 B. 9 C. 10 D. 11
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市公共交通收费如下:
公交票价
里程(千米)
票价(元)
刷卡优惠后付款(元)
0-10
2
1
10-15
3
1.5
15-20
4
2
20-25
5
2.5
25-30
6
3
以后每增加5千米
增加1元
增加0.5元
地铁票价
里程(千米)
票价(元)
0-6
3
6-12
4
12-22
5
22-32
6
32-52
7
52-72
8
以后每增加20千米
增加1元
(公交票价10千米(含)内2元,不足10千米按10千米计算,其他里程类同;地铁票价6千米(含)内3元,不足6千米按6千米计算,其他里程类同)
(1)张阿姨周日去看望父母,可是张阿姨忘了带一卡通,请你帮助张阿姨思考两个问题:
①若到父母家无论乘公交车还是地铁距离都是24千米,选择哪种公交交通工具费用较少?
②若只用10元钱乘坐公交或地铁,选择哪种公共交通工具乘坐的里程更远?
(2)张阿姨下周日计划使用一卡通刷卡乘公共交通到景点游玩,若里程大于35千米且小于120千米,公交、地铁均可直达.请问:选择公交还是选择地铁出行更省钱?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
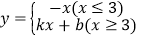 的图象经过第四象限的点B(3,a),且与x轴相交于原点和点A(7,0)
的图象经过第四象限的点B(3,a),且与x轴相交于原点和点A(7,0)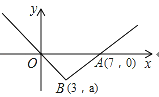
(1)求k、b的值;
(2)当x为何值时,y>﹣2;
(3)点C是坐标轴上的点,如果△ABC恰好是以AB为腰的等腰三角形,直接写出满足条件的点C的坐标
相关试题

