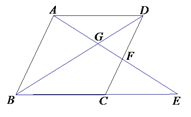
【题目】如图,在四边形ABCD中,AD//BC,E在BC的延长线,联结AE分别交BD、CD于点G、F,且![]() .
.
(1)求证:AB//CD;
(2)若![]() ,BG=GE,求证:四边形ABCD是菱形.
,BG=GE,求证:四边形ABCD是菱形.
参考答案:
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:
(1)由AD∥BC易得![]() ,结合
,结合![]() 可得
可得![]() ,由此即可得到AB∥CD;
,由此即可得到AB∥CD;
(2)结合已知和(1)中结论易得四边形ABCD是平行四边形,由此可得BC=AD,结合BC2=GD·BD可得![]() ,结合∠ADG=∠BDA可得△ADG∽△BDA,从而可得∠DAG=∠ABD,在证∠DAG=∠E,∠E=∠DBC,∠ABD=∠BDC即可得到∠BDC=∠DBC,从而可得BC=CD结合四边形ABCD是平行四边形即可得到结论了.
,结合∠ADG=∠BDA可得△ADG∽△BDA,从而可得∠DAG=∠ABD,在证∠DAG=∠E,∠E=∠DBC,∠ABD=∠BDC即可得到∠BDC=∠DBC,从而可得BC=CD结合四边形ABCD是平行四边形即可得到结论了.
试题解析:
(1)∵AD∥BC,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴AB∥CD;
(2)∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴BC=AD,
∵BC2=GD·BD,
∴AD2=GD·BD,即![]() ,
,
又∵∠ADG=∠BDA,
∴△ADG∽△BDA,
∴∠DAG=∠ABD,
∵AB∥CD,
∴∠ABD=∠BDC,
∵AD∥BC,
∴∠DAG=∠E,
∵BG=GE ,
∴∠DBC=∠E,
∴∠BDC=∠DBC,
∴BC=CD ,
∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形.
-
科目: 来源: 题型:
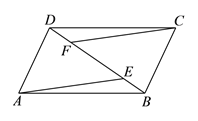
查看答案和解析>>【题目】已知:如图,E,F为□ABCD 的对角线BD上的两点,且BE=DF.
求证:AE∥CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游景点的年游客量y(万人)是门票价格x(元)的一次函数,其函数图像如下图.

(1)求y关于x的函数解析式;
(2)经过景点工作人员统计发现:每卖出一张门票所需成本为20元.那么要想获得年利润11500万元,且门票价格不得高于230元,该年的门票价格应该定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y = x上,那么称该菱形为点A,C的“极好菱形”. 下图为点A,C的“极好菱形”的一个示意图.
已知点M的坐标为(1,1),点P的坐标为(3,3).
(1)点E(2,1),F(1,3),G(4,0)中,能够成为点M,P的“极好菱形”的顶点的是 ;
(2)如果四边形MNPQ是点M,P的“极好菱形”.
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;

②当四边形MNPQ的面积为8,且与直线y = x + b有公共点时,写出b的取值范围.
-
科目: 来源: 题型:
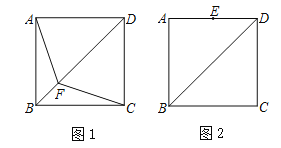
查看答案和解析>>【题目】已知:如图,正方形ABCD中,点F是对角线BD上的一个动点.
(1)如图1,连接AF,CF,直接写出AF与CF的数量关系;
(2)如图2,点E为AD边的中点,当点F运动到线段EC上时,连接AF,BE相交于点O.
①请你根据题意在图2中补全图形;
②猜想AF与BE的位置关系,并写出证明此猜想的思路;
③如果正方形的边长为2,直接写出AO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某施工小组乘-辆汽车在东西走向的公路上进行建设,约定向东走为正,某大从
 地出发到收工时的行走记录如下(单位:
地出发到收工时的行走记录如下(单位: 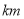 );
);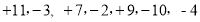 ,
,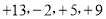 ,求:
,求:(1)问收工时施工小组是否回到
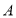 地,如果回到
地,如果回到 地,请说明理由;如果没有回到
地,请说明理由;如果没有回到 地,请说明检修小组最后的位置:
地,请说明检修小组最后的位置:(2)距离
 地最远的是哪一次?距离多远?
地最远的是哪一次?距离多远?(3)若汽车每千米耗油
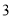 升,开工时储油
升,开工时储油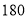 升,到收工时,中途是否需要加油,若加油最少加多少升?若不需要加油,到收工时,还剩多少升汽油? (假定汽车可以开到油量为
升,到收工时,中途是否需要加油,若加油最少加多少升?若不需要加油,到收工时,还剩多少升汽油? (假定汽车可以开到油量为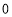 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要从甲乙两名射击运动员中挑选一人参加全市比赛,在选拔赛中,每人进行了5次射击,甲的成绩(环)为:9.7,10,9.6,9.8,9.9;乙的成绩的平均数为9.8,方差为0.032;
(1)甲的射击成绩的平均数和方差分别是多少?
(2)据估计,如果成绩的平均数达到9.8环就可能夺得金牌,为了夺得金牌,应选谁参加比赛?
相关试题

