【题目】某施工小组乘-辆汽车在东西走向的公路上进行建设,约定向东走为正,某大从![]() 地出发到收工时的行走记录如下(单位:
地出发到收工时的行走记录如下(单位: ![]() );
);![]() ,
,![]() ,求:
,求:
(1)问收工时施工小组是否回到![]() 地,如果回到
地,如果回到![]() 地,请说明理由;如果没有回到
地,请说明理由;如果没有回到![]() 地,请说明检修小组最后的位置:
地,请说明检修小组最后的位置:
(2)距离![]() 地最远的是哪一次?距离多远?
地最远的是哪一次?距离多远?
(3)若汽车每千米耗油![]() 升,开工时储油
升,开工时储油![]() 升,到收工时,中途是否需要加油,若加油最少加多少升?若不需要加油,到收工时,还剩多少升汽油? (假定汽车可以开到油量为
升,到收工时,中途是否需要加油,若加油最少加多少升?若不需要加油,到收工时,还剩多少升汽油? (假定汽车可以开到油量为![]() )
)
参考答案:
【答案】(1)没有回到![]() 地.距离
地.距离![]() 地东
地东![]() ;(2)距离
;(2)距离![]() 地最远的是第
地最远的是第![]() 次.距离
次.距离![]() 地
地![]() ;(3)需要加油,需加油
;(3)需要加油,需加油![]() 升
升
【解析】
(1)根据题目中的数据可以解答本题;
(2)根据题目中的数据可以求得每次所在的位置,从而可以解答本题;
(3)根据题意可以求得行驶的总路程,从而可以解答本题.
解:(1)![]() +(-4)+(+13)+(-2)+(+5)+(+9)
+(-4)+(+13)+(-2)+(+5)+(+9)
=11-3+7-2+9-10-4+13-2+5+9
![]()
没有回到![]() 地.距离
地.距离![]() 地东
地东![]() .
.
(2) 第一次为11千米,
第二次是113=8千米,
第三次是8+7=15千米,
第四次为152=13千米,
第五次为13+9=22千米,
第六次为2210=12千米,
第七次为124=8千米,
第八次为8+13=21千米,
第九次为21-2=19千米,
第十次为19+5=24千米,
第十一次为24+9=33千米,
即距A地最远的是第十一次;距离![]() 地最远的是第
地最远的是第![]() 次.距离
次.距离![]() 地
地![]() .
.
(3)![]()
![]()
![]()
![]()
![]() 需要加油.
需要加油.
![]() (升)
(升)
即需加油![]() 升.
升.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y = x上,那么称该菱形为点A,C的“极好菱形”. 下图为点A,C的“极好菱形”的一个示意图.
已知点M的坐标为(1,1),点P的坐标为(3,3).
(1)点E(2,1),F(1,3),G(4,0)中,能够成为点M,P的“极好菱形”的顶点的是 ;
(2)如果四边形MNPQ是点M,P的“极好菱形”.
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;

②当四边形MNPQ的面积为8,且与直线y = x + b有公共点时,写出b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD//BC,E在BC的延长线,联结AE分别交BD、CD于点G、F,且
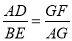 .
.(1)求证:AB//CD;
(2)若
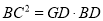 ,BG=GE,求证:四边形ABCD是菱形.
,BG=GE,求证:四边形ABCD是菱形.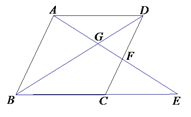
-
科目: 来源: 题型:
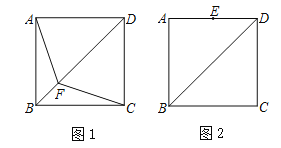
查看答案和解析>>【题目】已知:如图,正方形ABCD中,点F是对角线BD上的一个动点.
(1)如图1,连接AF,CF,直接写出AF与CF的数量关系;
(2)如图2,点E为AD边的中点,当点F运动到线段EC上时,连接AF,BE相交于点O.
①请你根据题意在图2中补全图形;
②猜想AF与BE的位置关系,并写出证明此猜想的思路;
③如果正方形的边长为2,直接写出AO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要从甲乙两名射击运动员中挑选一人参加全市比赛,在选拔赛中,每人进行了5次射击,甲的成绩(环)为:9.7,10,9.6,9.8,9.9;乙的成绩的平均数为9.8,方差为0.032;
(1)甲的射击成绩的平均数和方差分别是多少?
(2)据估计,如果成绩的平均数达到9.8环就可能夺得金牌,为了夺得金牌,应选谁参加比赛?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在直角坐标平面内,抛物线
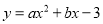 与
与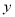 轴交于点A,与x轴分别交于点B(-1,0)、点C(3,0),点D是抛物线的顶点.
轴交于点A,与x轴分别交于点B(-1,0)、点C(3,0),点D是抛物线的顶点.(1)求抛物线的表达式及顶点D的坐标;
(2)连接AD、DC,求
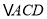 的面积;
的面积;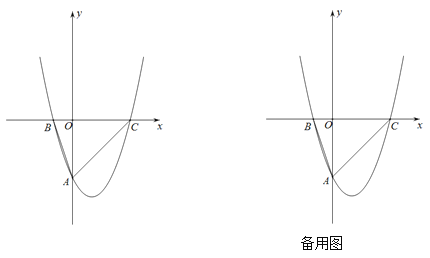
(3)点P在直线DC上,联结OP,若以O、P、C为顶点的三角形与△ABC相似,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索与猜想:
有一列数: 第一个数是
 ,第二个数
,第二个数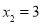 ,第三个数开始依次记为
,第三个数开始依次记为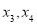 、..从第二个数开始,每个数是它相邻两数和的一半.
、..从第二个数开始,每个数是它相邻两数和的一半.(1)则第三、四、五个数分别为 、 、 ;
(2)推测
 ______ ;
______ ;(3)猜想第
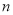 个数
个数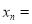 .
.(4)计算:

相关试题

