【题目】某旅游景点的年游客量y(万人)是门票价格x(元)的一次函数,其函数图像如下图.

(1)求y关于x的函数解析式;
(2)经过景点工作人员统计发现:每卖出一张门票所需成本为20元.那么要想获得年利润11500万元,且门票价格不得高于230元,该年的门票价格应该定为多少元?
参考答案:
【答案】(1)y=-x+300(2)70
【解析】试题分析:
(1)设y与x的函数关系式为:y=kx+b,代入图中两点的坐标,列出方程组,解方程组求得k、b的值,即可得到所求的解析式;
(2)设门票价格定为x元,结合(1)可列出方程(x-20)(-x+300)=11500,解方程即可.
试题解析:
(1)设![]() ,函数图像过点(200,100), (50,250)
,函数图像过点(200,100), (50,250)
代入解析式得: ![]() ,解得:
,解得: ![]() ,
,
∴y关于x的解析式为: ![]() ;
;
(2)设门票价格定为x元,依题意可得:
![]() ,
,
整理得: ![]() , 解之得:x=70或者x=250(舍去),
, 解之得:x=70或者x=250(舍去),
答:门票价格应该定为70元.
-
科目: 来源: 题型:
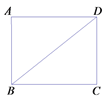
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的长为1,点P是线段BD上的一点,联结CP,将△BCP沿着直线CP翻折,若点B落在边AD上的点E处,且EP//AB,则AB的长等于________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,点D在BA的延长线上,BC=24,
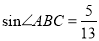 .
.(1)求AB的长;
(2)若AD=6.5,求
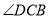 的余切值.
的余切值.
-
科目: 来源: 题型:
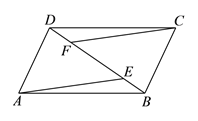
查看答案和解析>>【题目】已知:如图,E,F为□ABCD 的对角线BD上的两点,且BE=DF.
求证:AE∥CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y = x上,那么称该菱形为点A,C的“极好菱形”. 下图为点A,C的“极好菱形”的一个示意图.
已知点M的坐标为(1,1),点P的坐标为(3,3).
(1)点E(2,1),F(1,3),G(4,0)中,能够成为点M,P的“极好菱形”的顶点的是 ;
(2)如果四边形MNPQ是点M,P的“极好菱形”.
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;

②当四边形MNPQ的面积为8,且与直线y = x + b有公共点时,写出b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD//BC,E在BC的延长线,联结AE分别交BD、CD于点G、F,且
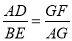 .
.(1)求证:AB//CD;
(2)若
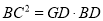 ,BG=GE,求证:四边形ABCD是菱形.
,BG=GE,求证:四边形ABCD是菱形.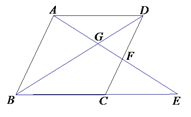
-
科目: 来源: 题型:
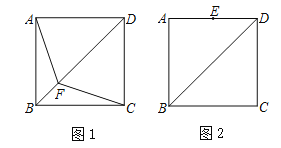
查看答案和解析>>【题目】已知:如图,正方形ABCD中,点F是对角线BD上的一个动点.
(1)如图1,连接AF,CF,直接写出AF与CF的数量关系;
(2)如图2,点E为AD边的中点,当点F运动到线段EC上时,连接AF,BE相交于点O.
①请你根据题意在图2中补全图形;
②猜想AF与BE的位置关系,并写出证明此猜想的思路;
③如果正方形的边长为2,直接写出AO的长.
相关试题

