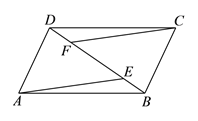
【题目】已知:如图,E,F为□ABCD 的对角线BD上的两点,且BE=DF.
求证:AE∥CF.
参考答案:
【答案】证明见解析
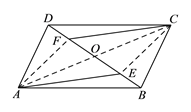
【解析】试题分析:连接AC交BD于点O,连接AF,CE,根据平行四边形的对角线互相平分可得OB=OD,OA=OC,再由BE=DF,可得OE=OF,根据对角线互相平分的四边形是平行四边形可判定四边形AECF是平行四边形,所以AE∥CF.
试题解析:
证明:连接AC交BD于点O,
连接AF,CE.
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC.(平行四边形的对角线互相平分)
∵BE=DF,∴OB-BE=OD-DF
即OE=OF.
∴四边形AECF是平行四边形.(对角线互相平分的四边形是平行四边形)
∴AE∥CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某银行去年新增加居民存款10亿元人民币.
(1)经测量,100张面值为100元的新版人民币大约厚0.9厘米,如果将10亿元面值为100元的新版人民币摞起来,大约有多高?
(2)一台激光点钞机的点钞速度是8×104张/时,按每天点钞5小时计算,如果让点钞机点一遍10亿元面值为100元的新版人民币,点钞机大约要点多少天?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论:①若
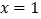 是关于x的方程a
是关于x的方程a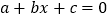 的一个解,则
的一个解,则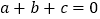 ;②若
;②若 ,则关于x的方程
,则关于x的方程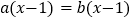 有唯一的解;③若
有唯一的解;③若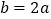 ,则关于x的方程
,则关于x的方程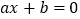 (
(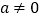 )的解为
)的解为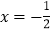 ;④若
;④若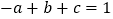 ,且
,且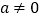 ,则
,则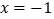 一定是方程
一定是方程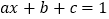 的解.其中,结论正确的有( )
的解.其中,结论正确的有( )A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
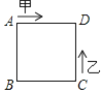
A. AB B. BC C. CD D. DA
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,BD平分∠ABC.过点D作AB的平行线,过点B作AC的平行线,两平行线相交于点E, BC交DE于点F,连接CE.求证:四边形BECD是矩形.
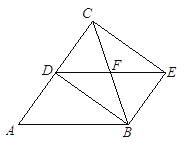
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好的保护美丽图画的邛海湿地,西昌市污水处理厂决定先购买A、B两型污水处理设备共20台,对邛海湿地周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在10cm高度处连通(即管子底部离容器底10cm),现三个容器中,只有乙中有水,水位高4cm,如图所示.若每分钟同时向甲和丙注入相同量的水,开始注水1分钟,甲的水位上升3cm.则开始注入 分钟水量后,甲的水位比乙高1cm.

相关试题

