【题目】已知![]() 四个点.
四个点.
(1)在图中描出![]() ,
,![]() ,
,![]() ,
,![]() 四个点,顺次连接
四个点,顺次连接![]() 四点;
四点;
(2)直接写出线段![]() 之间的位置关系_____________;
之间的位置关系_____________;
(3)求四边形![]() 的面积
的面积
(4)将四边形![]() 向右平移2个单位长度,向上平移4个单位长度得到四边形
向右平移2个单位长度,向上平移4个单位长度得到四边形![]() 写出各顶点坐标
写出各顶点坐标![]() ___________,
___________,![]() ____________,
____________,![]() ____________,
____________,![]() ____________.
____________.

参考答案:
【答案】(1)见解析;(2)AB∥CD且AB=CD;(3)15;(4)![]() 坐标为(-1,2),
坐标为(-1,2),![]() 坐标为(4,2),
坐标为(4,2),![]() 坐标为(5,5),
坐标为(5,5),![]() 坐标为(0,5).
坐标为(0,5).
【解析】
(1)根据A(-3,-2),B(2,-2),C(3,1),D(-2,1),在图中描出A,B,C,D四个点,并顺次连接点A,B,C,D,A即可.
(2)根据图示,写出线段AB,CD之间的位置关系和数量关系即可.
(3)根据平行四边形的面积=底×高,求出四边形ABCD的面积是多少即可.
(4)找到向右平移2个单位长度,向上平移4个单位长度后各点的对应点,可得出点各点的坐标.
解:(1)
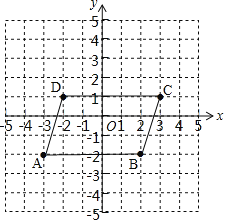 .
.
(2)AB,CD之间的关系是:
AB∥CD且AB=CD.
(3)[2-(-3)]×[1-(-2)]
=5×3
=15
答:四边形ABCD的面积是15.
(4)![]() 坐标为(-1,2),
坐标为(-1,2),![]() 坐标为(4,2),
坐标为(4,2),![]() 坐标为(5,5),
坐标为(5,5),![]() 坐标为(0,5).
坐标为(0,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B为中点.

(Ⅰ)计算AB的长等于;
(Ⅱ)若点P,Q分别为线段BC,AC上的动点,且BP=CQ,请在如图所示的网格中,用无刻度的直尺,画出当PQ最短时,点P,Q的位置,并简要说明画图方法(不要求证明) . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,顶点A、B的坐标分别是A(1,0),B(0,﹣2),顶点C、D在双曲线
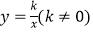 上,边AD与y轴相交于点E,
上,边AD与y轴相交于点E, 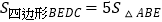 =10,则k的值是( )
=10,则k的值是( )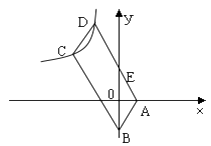
A.-16
B.-9
C.-8
D.-12 -
科目: 来源: 题型:
查看答案和解析>>【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

-
科目: 来源: 题型:
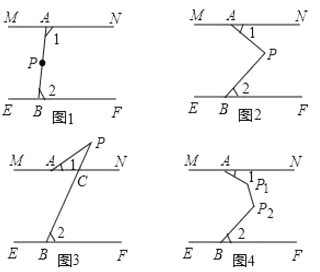
查看答案和解析>>【题目】如图1,将两根笔直的细木条
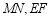 用图钉固定并平行摆放,将一根橡皮筋拉直后用图有分别周定在
用图钉固定并平行摆放,将一根橡皮筋拉直后用图有分别周定在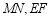 上,橡皮筋的两端点分别记为点
上,橡皮筋的两端点分别记为点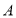 ,点
,点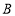 .
.(1)图1中,点
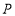 在
在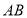 上,若
上,若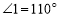 ,则
,则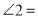 ___________
___________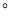 ;
;(2)
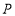 为橡皮筋上一点,,用橡皮筋的弹性拉动橡皮筋,使
为橡皮筋上一点,,用橡皮筋的弹性拉动橡皮筋,使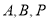 三点不在同一直线,后用图固定点
三点不在同一直线,后用图固定点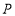 .
.①如图2,若点
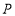 在两根细木条所在直线之间,且
在两根细木条所在直线之间,且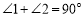 ,试判断线段
,试判断线段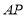 与
与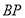 所在直线的位置关系,并说明理由;
所在直线的位置关系,并说明理由;②如图3,若点
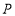 在两根细木条所在直线的同侧,且
在两根细木条所在直线的同侧,且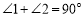 ,
,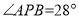 ,试求
,试求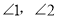 的度数;
的度数;(3)如图4,
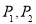 为AB上两点,拉动橡皮筋并固定,若
为AB上两点,拉动橡皮筋并固定,若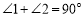 ,则
,则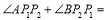 ____________
____________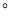 .
. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折, 使点A落在BC边上的点F处,则CE的最大值为( )

A.
B.
C.4
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个)
8
7
6
5
4
3
人数
2
1
4
7
8
2
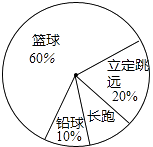
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为个;进球数的中位数为个,众数为个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数).
相关试题

