【题目】如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折, 使点A落在BC边上的点F处,则CE的最大值为( )
A.![]()
B.![]()
C.4
D.![]()
参考答案:
【答案】B
【解析】过点E作EM⊥BC于M,连接EF,

由已知可知EF=AE,设CE=x ,则AE=AC-CE=8-x,
∴EF=8-x,
∵∠C=30°,
∴EM= ![]() CE=
CE= ![]() x,
x,
又∵EM≤EF,
∴ ![]() x≤8-x,
x≤8-x,
∴x≤ ![]() ,即CE的最大值是
,即CE的最大值是 ![]() ;
;
所以答案是:B.
【考点精析】解答此题的关键在于理解垂线段最短的相关知识,掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用,以及对线段垂直平分线的性质的理解,了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 四个点.
四个点.(1)在图中描出
 ,
, ,
, ,
, 四个点,顺次连接
四个点,顺次连接 四点;
四点;(2)直接写出线段
 之间的位置关系_____________;
之间的位置关系_____________;(3)求四边形
 的面积
的面积(4)将四边形
 向右平移2个单位长度,向上平移4个单位长度得到四边形
向右平移2个单位长度,向上平移4个单位长度得到四边形 写出各顶点坐标
写出各顶点坐标 ___________,
___________, ____________,
____________, ____________,
____________, ____________.
____________.
-
科目: 来源: 题型:
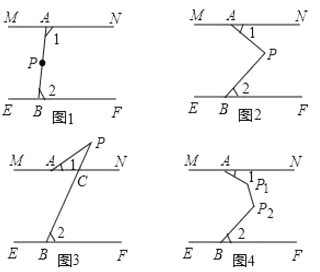
查看答案和解析>>【题目】如图1,将两根笔直的细木条
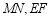 用图钉固定并平行摆放,将一根橡皮筋拉直后用图有分别周定在
用图钉固定并平行摆放,将一根橡皮筋拉直后用图有分别周定在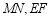 上,橡皮筋的两端点分别记为点
上,橡皮筋的两端点分别记为点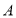 ,点
,点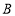 .
.(1)图1中,点
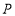 在
在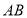 上,若
上,若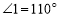 ,则
,则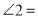 ___________
___________ ;
;(2)
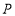 为橡皮筋上一点,,用橡皮筋的弹性拉动橡皮筋,使
为橡皮筋上一点,,用橡皮筋的弹性拉动橡皮筋,使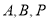 三点不在同一直线,后用图固定点
三点不在同一直线,后用图固定点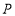 .
.①如图2,若点
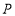 在两根细木条所在直线之间,且
在两根细木条所在直线之间,且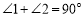 ,试判断线段
,试判断线段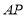 与
与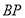 所在直线的位置关系,并说明理由;
所在直线的位置关系,并说明理由;②如图3,若点
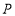 在两根细木条所在直线的同侧,且
在两根细木条所在直线的同侧,且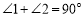 ,
,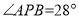 ,试求
,试求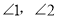 的度数;
的度数;(3)如图4,
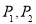 为AB上两点,拉动橡皮筋并固定,若
为AB上两点,拉动橡皮筋并固定,若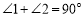 ,则
,则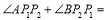 ____________
____________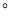 .
. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个)
8
7
6
5
4
3
人数
2
1
4
7
8
2
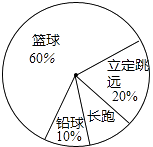
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为个;进球数的中位数为个,众数为个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
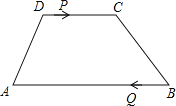
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠ACB=90°,AC=2,CB=4.点P为线段CB上一动点,连接AP,△APC与△APC′关于直线AP对称,其中点C的对称点为点C′.直线m过点A且平行于CB
(1)如图①:连接AB,当点C落在线段AB上时,求BC′的长;
(2)如图②:当PC=
 BC时,延长PC′交直线m于点D,求△ADC′面积;
BC时,延长PC′交直线m于点D,求△ADC′面积;(3)在(2)的条件下,连接BC′,直接写出线段BC′的长.

相关试题

